- CG
- (Conjugate Gradient acceleration): This is the two-term form of conjugate gradient for symmetric and positive definite (SPD) matrices and mildly nonsymmetric matrices. Only left preconditioning is allowed.
- SI
- (Chebyshev acceleration or Semi-Iteration): This is the two-term form of Chebyshev acceleration for the same general class of matrices as CG. Only left preconditioning is allowed.
- SOR
- (Successive Overrelaxation):
This routine must be used as
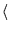 accel
accel 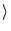 for the SOR algorithm with adaptive parameter determination.
It is intended for SPD and mildly
nonsymmetric matrices. For this choice of
for the SOR algorithm with adaptive parameter determination.
It is intended for SPD and mildly
nonsymmetric matrices. For this choice of
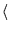 accel
accel 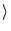 ,
,
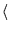 precon
precon 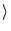 is restricted to SORi and LSORi for allowed values
of i. Also, these choices of
is restricted to SORi and LSORi for allowed values
of i. Also, these choices of 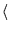 precon
precon 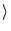 cannot be used with other accelerations since SOR cannot
be accelerated. Note that Successive Overrelaxation is
not an acceleration but is included here since the
function of the SOR module is analogous to that of an
cannot be used with other accelerations since SOR cannot
be accelerated. Note that Successive Overrelaxation is
not an acceleration but is included here since the
function of the SOR module is analogous to that of an
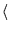 accel
accel 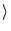 module.
module.
- SRCG
- (SSOR CG Algorithm):
This algorithm performs the SSOR conjugate gradient
algorithm with an adaptive procedure for
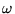 .
It is
intended for SPD and mildly nonsymmetric matrices.
.
It is
intended for SPD and mildly nonsymmetric matrices.
 precon
precon 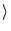 is restricted to SSORi and
LSSORi for allowed values of i. These selections
for
is restricted to SSORi and
LSSORi for allowed values of i. These selections
for 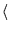 precon
precon 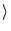 can also be used with other
accelerators, but no adapting on
can also be used with other
accelerators, but no adapting on 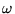 will be performed.
Only left preconditioning is allowed. Note that the SRCG
module combines both an accelerator and a preconditioner
but is included here since its function is analogous to
that of an
will be performed.
Only left preconditioning is allowed. Note that the SRCG
module combines both an accelerator and a preconditioner
but is included here since its function is analogous to
that of an 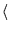 accel
accel 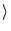 module.
module.
- SRSI
- (SSOR SI Algorithm):
This algorithm performs the SSOR semi-iteration
algorithm with an adaptive procedure for
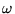 .
It is
intended for SPD and mildly nonsymmetric matrices.
.
It is
intended for SPD and mildly nonsymmetric matrices.
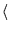 precon
precon 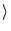 is restricted to SSORi and
LSSORi for allowed values of i. Only left
preconditioning is allowed. Note that the SRSI module
combines both an accelerator and a preconditioner but is
included here since its function is analogous to that of
an
is restricted to SSORi and
LSSORi for allowed values of i. Only left
preconditioning is allowed. Note that the SRSI module
combines both an accelerator and a preconditioner but is
included here since its function is analogous to that of
an 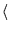 accel
accel 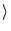 module.
module.
- BASIC
- (Basic Iterative Method):
This algorithm runs the unaccelerated iterative method
corresponding to the given preconditioner. The default
extrapolation factor used in BASIC is 2/(EMAX+EMIN) where
EMAX and EMIN are RPARM variables. To run the unaccelerated
method with no extrapolation, EMAX and EMIN should be
set to 1. Only left preconditioning is allowed.
Note that the BASIC module is not an accelerator
but is included here since its function is analogous
to that of an
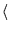 accel
accel  module.
module.
- ME
- (Minimal Error Algorithm):
This is an ORTHODIR-like algorithm for symmetric systems
with a three term recurrence which minimizes
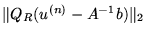 ,
the 2-norm of the error,
at each iteration [8].
,
the 2-norm of the error,
at each iteration [8].
- CGNR
- (Conjugate Gradient applied to the Normal Equations):
This implementation of CG applied to the normal equations
of the preconditioned system minimizes
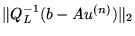 ,
the 2-norm of the residual
vector of the original preconditioned system, at each iteration
[22]. Only left preconditioning is allowed.
,
the 2-norm of the residual
vector of the original preconditioned system, at each iteration
[22]. Only left preconditioning is allowed.
- LSQR
- (Least Squares Algorithm): This algorithm calculates the same iterates as CGNR but in a slightly more stable fashion [22]. Only left preconditioning is allowed.
- ODIR
- (ORTHODIR): This is a truncated/restarted method useful for nonsymmetric systems of equations [36]. The user can specify the number of old vectors used in the truncation and the restarting frequency.
- OMIN
- (ORTHOMIN): This is a common truncated/restarted method used for nonsymmetric systems [36]. Note that this method includes the popular GCR method (Generalized Conjugate Residual or restarted ORTHOMIN) [7].
- ORES
- (ORTHORES): This is another truncated/restarted method for nonsymmetric systems [36].
- IOM
- (Incomplete Orthogonalization Method): This is a truncated method due to Saad [25,26] which calculates the same iterates, in exact arithmetic, as ORTHORES. In the symmetric case, it runs the SYMMLQ algorithm of Paige and Saunders [21]. Only left preconditioning is allowed.
- GMRES
- (Generalized Minimal Residual Method):
This method is a truncated/restarted method which, in the
case of pure restarting (NS2
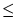 NS1 +1 where NS1
and NS2 are IPARM quantities), calculates
the same iterates as the truncated/restarted ORTHODIR algorithm
[27]. In the symmetric case, it may be used to run
the MINRES algorithm of Paige and Saunders [21].
NS1 +1 where NS1
and NS2 are IPARM quantities), calculates
the same iterates as the truncated/restarted ORTHODIR algorithm
[27]. In the symmetric case, it may be used to run
the MINRES algorithm of Paige and Saunders [21].
- USYMLQ
- (Unsymmetric LQ): This is a quasi-Krylov method useful for nonsymmetric systems [34]. Only left preconditioning is allowed.
- USYMQR
- (Unsymmetric QR): This is a companion algorithm to USYMLQ. It minimizes the 2-norm of the residual over an appropriate quasi-Krylov space [34]. Only left preconditioning is allowed.
- LANDIR
- (Lanczos/ORTHODIR): This is the first of the three variants of the Lanczos algorithm for nonsymmetric systems [11]. Only left preconditioning is allowed.
- LANMIN
- (Lanczos/ORTHOMIN or Biconjugate Gradient Method): This second variant of the Lanczos algorithm does slightly less work per iteration than the other variants of the Lanczos method and is often referred to as the Biconjugate gradient method [11].
- LANRES
- (Lanczos/ORTHORES or ``two-sided" Lanczos Method): This method is the third variant of the Lanczos algorithm [11]. Only left preconditioning is allowed.
- CGCR
- (Constrained Generalized Conjugate Residual Method):
This method couples truncated/restarted ORTHOMIN with
a constrained residual technique described in
[32,33].
At each iteration, the average residual over each
two-dimensional block is forced to be zero. The
variable NBL2D must be appropriately set for this algorithm.
- BCGS
- (Biconjugate Gradient Squared Method): This method is similar to the Biconjugate Gradient Method, and in many cases performs better [12]. Only left preconditioning is implemented.
|
The permitted
|