Homework for SPAN

1. When is a vector an element of a span?

• Examples:
  • From http://linear.pugetsound.edu/html/section-S.html , read Example LCM, Example SSP, and Example SM32.
    Note: Beezer uses the notation $\langle S \rangle$ for $\textrm{Span}(S).$ We will use the latter.
  • Example: Let $\mathcal{F}_2 = \left\{ \cos(2t) , \sin(2t), 1 \right\} \subseteq C^{\ \infty}(\mathbb{R}).$ Use the power reduction formulas to show $\cos^2(t) \in \textrm{Span}(\mathcal{F}_2).$
    Solution: The power reduction formula for $\cos^2(t)$ gives us $$\cos^2(t) = \frac{1 + \cos(2t)}{2} = \frac{1}{2} (1) + \frac{1}{2} (\cos(2t))$$ which is a linear combination of the vectors $1$ and $\cos(2t) \in \mathcal{F}_2,$ thus $\cos^2(t) \in \textrm{Span}(\mathcal{F}_2).$
• Homework:
  • From http://linear.pugetsound.edu/html/section-S.html , do Exercises S.C15, S.C16, S.C17, S.C20, and S.C21.
    Note: For Exercises S.C16, S.C17, and S.C21, express the vector ${\bf v}$ as a linear combination of vectors from the set $S.$
  • Find the appropriate formulas here:
    • https://en.wikipedia.org/wiki/List_of_trigonometric_identities
    • https://en.wikipedia.org/wiki/Taylor_series
    1. Let $\mathcal{F}_2 = \left\{ \cos(2t) , \sin(2t), 1 \right\}$ and $\mathcal{T}_2 = \left\{ \cos^2(t) , \cos(t) \sin(t), \sin^2(t) \right\}.$ Use the power reduction formulas and the double angle identities to show the following:
       1. Show $\mathcal{T}_2 \subseteq \textrm{Span}(\mathcal{F}_2).$
       2. Show $\mathcal{F}_2 \subseteq \textrm{Span}(\mathcal{T}_2).$
       Note: These two facts along with Theorem 2 show that $\textrm{Span}(\mathcal{T}_2) = \textrm{Span}(\mathcal{F}_2).$
    2. Let $\mathcal{F}_3 = \left\{ \cos(t) , \sin(t) , \cos(3t) , \sin(3t) \right\}$ and $\mathcal{T}_3 = \left\{ \cos^3(t) , \cos^2(t) \sin(t) , \cos(t) \sin^2(t) , \sin^3(t) \right\}.$ Use the power reduction formulas and the triple angle identities to show the following:
       1. Show $\mathcal{T}_3 \subseteq \textrm{Span}(\mathcal{F}_3).$
       2. Show $\mathcal{F}_3 \subseteq \textrm{Span}(\mathcal{T}_3).$
       Note: These two facts along with Theorem 2 show that $\textrm{Span}(\mathcal{T}_3) = \textrm{Span}(\mathcal{F}_3).$
    3. Let $\mathcal{M}_0 = \left\{ 1 , t , t^2 , t^3 \right\}$ and $\mathcal{M}_1 = \left\{ 1 , (t-1) , (t-1)^2 , (t-1)^3 \right\}.$ Use the Taylor Series Formula to show the following:
       1. Show $\mathcal{M}_1 \subseteq \textrm{Span}(\mathcal{M}_0).$
       2. Show $\mathcal{M}_0 \subseteq \textrm{Span}(\mathcal{M}_1).$
       Note: These two facts along with Theorem 2 show that $\textrm{Span}(\mathcal{M}_1) = \textrm{Span}(\mathcal{M}_0) = \mathcal{P}_3.$

2. Is $\textrm{Span}(S) \subseteq W?$

• Examples:
  • Example A: Let $$S = \left\{ \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right] , \left[ \begin{array}{c} -2e^{3t} \\ e^{3t} \\ \end{array} \right] \right\} \subseteq C^{\infty}(\mathbb{R},\mathbb{R}^2) \quad \textrm{ and } \quad A = \left[ \begin{array}{cc} 5 & 4 \\ -2 & -1 \\ \end{array} \right].$$ Is $\textrm{Span}(S) \subseteq V_A?$
    Solution: We can check that $S \subseteq V_A$ by plugging each vector in $S$ into the equation $\frac{d}{dt} {\bf x} = A {\bf x}:$
    • $$\frac{d}{dt} \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right] = \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right], \quad \textrm{ and } \quad \left[ \begin{array}{cc} 5 & 4 \\ -2 & -1 \\ \end{array} \right] \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right] = \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right], \quad \textrm{ thus } \quad \left[ \begin{array}{c} -e^t \\ e^t \\ \end{array} \right] \in V_A.$$
    • $$\frac{d}{dt} \left[ \begin{array}{c} -2e^{3t} \\ e^{3t} \\ \end{array} \right] = \left[ \begin{array}{c} -6e^{3t} \\ 3e^{3t} \\ \end{array} \right], \quad \textrm{ and } \quad \left[ \begin{array}{cc} 5 & 4 \\ -2 & -1 \\ \end{array} \right] \left[ \begin{array}{c} -2e^{3t} \\ e^{3t} \\ \end{array} \right] = \left[ \begin{array}{c} -6e^{3t} \\ 3e^{3t} \\ \end{array} \right], \quad \textrm{ thus } \quad \left[ \begin{array}{c} -2e^{3t} \\ e^{3t} \\ \end{array} \right] \in V_A.$$
    • Thus $S \subseteq V_A,$ and $V_A \subseteq C^{\infty}(\mathbb{R},\mathbb{R}^2)$ is a subspace, so by Theorem 2, $\textrm{Span}(S) \subseteq V_A.$
  • The general outline for solving such a problem is as follows:
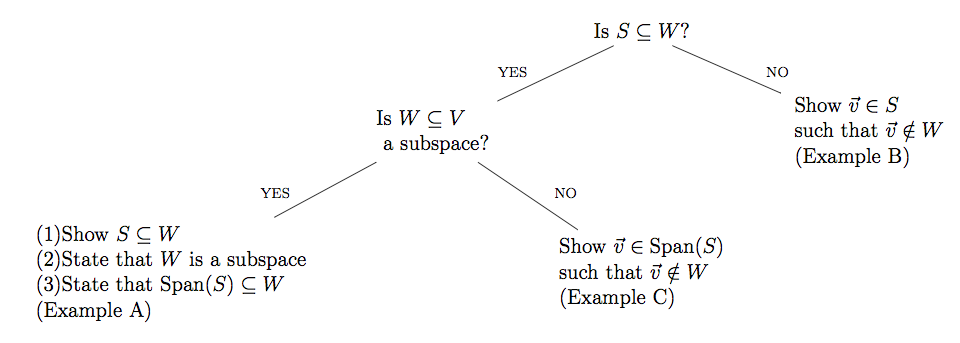
  • Example B: Let $$S = \left\{ \ \left[ \begin{array}{c} 1 \\ -1 \\ 0 \\ \end{array} \right] , \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ \end{array} \right] \ \right\} \subseteq \mathbb{R}^3 \quad \textrm{ and } \quad A = \left[ \begin{array}{ccc} 3 & 3 & -3 \\ -1 & -1 & 1 \\ -2 & 2 & 2 \end{array} \right].$$ Is $\textrm{Span}(S) \subseteq \textrm{Nul}(A)?$
    Solution: It is the case that the second vector in $S$ is in fact in $\textrm{Nul}(A),$ but the first vector is not: $$\left[ \begin{array}{ccc} 3 & 3 & -3 \\ -1 & -1 & 1 \\ -2 & 2 & 2 \end{array} \right] \left[ \begin{array}{c} 1 \\ -1 \\ 0 \\ \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ -4 \\ \end{array} \right] \neq \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right],$$ thus $S$ is not a subset of $\textrm{Nul}(A),$ and so $\textrm{Span}(S)$ is not a subset of $\textrm{Nul}(A).$
  • Example C: Let $S = \left\{ [-1,1] , [1,1] \right\} \subseteq \mathbb{R}^2$ and $W = \left\{ [x,y] \in \mathbb{R}^2 \, \middle\vert \, x^2=y^2 \right\}.$ Is $\textrm{Span}(S) \subseteq W?$
    Solution: In this case, $S$ is a subset of $W.$ However, $W$ is not a subspace, and is not closed under taking linear combinations. Our goal is to take a linear combination of the two vectors in $S$, $\alpha [-1,1] + \beta [1,1],$ such that this linear combination is not in $W.$ Here, we can simply let $\alpha = 1$ and $\beta = 1.$ Then $[-1,1]+[1,1]=[0,2] \notin W$ since $(0)^2 \neq (2)^2.$ Thus $\textrm{Span}(S)$ is not a subset of $W.$
• Homework: For each of the following, emulate the above examples. Determine the example type (A, B, or C) and use the associated technique to prove or disprove $\textrm{Span}(S) \subseteq W.$
  • 1. Let $S = \left\{ e^{2t} \right\}$ and $W = \left\{ y \ \middle\vert \ y^{\ \prime \prime} + y = 5 e^{2t} \right\}.$
    2. Let $S = \left\{ \cos(t) \right\}$ and $W = \left\{ y \ \middle\vert \ y^{\ \prime \prime} + y = 0 \textrm{ and } y^{\ \prime}(0) = 0 \right\}.$
    3. Let $S = \left\{ \cos(t) \right\}$ and $W = \left\{ y \ \middle\vert \ y^{\ \prime \prime} + y = 0 \textrm{ and } y(0) = 1 \right\}.$
    4. Let $S = \left\{ \sin(t) \right\}$ and $W = \left\{ y \ \middle\vert \ y^{\ \prime \prime} + y = 0 \textrm{ and } y^{\ \prime}(0) = 0 \right\}.$
    5. Let $$S = \left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \right\} \textrm{ and } W = \left\{ A \in M_2(\mathbb{R}) \ \middle\vert \ \det(A) \neq 0 \right\}.$$
    6. Let $$S = \left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array} \right] , \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ \end{array} \right] \right\} \textrm{ and } W = \left\{ A \in M_2(\mathbb{R}) \ \middle\vert \ \det(A) = 0 \right\}.$$
    7. Let $$S = \left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & -1 \\ \end{array} \right] , \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right] \right\} \textrm{ and } W = \left\{ A = \left[ \begin{array}{cc} a & b \\ c & d \\ \end{array} \right] \ \middle\vert \ \textrm{trace}(A) = a + d = 0 \right\}.$$
    8. Let $$S = \left\{ \left[ \begin{array}{c} \cos(t) \\ -\sin(t) \\ \end{array} \right] , \left[ \begin{array}{c} -\sin(t) \\ \cos(t) \\ \end{array} \right] \right\} \textrm{ and } W = V_A \textrm{ with } A = \left[ \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right].$$

3. Find a spanning set for $V.$

• Examples:
  • Example: Let $V = \left\{ p \in \mathcal{P}_3 \ \middle\vert \ p(2) = p(0) \textrm{ and } p^{\ \prime}(1) = 0 \right\}.$ Find a spanning set $S$ for $V$.
    Solution: If $p \in \mathcal{P}_3,$ we can express $p$ as $$p(t) = a_3 t^3 + a_2 t^2 + a_1 t + a_0.$$ Then $$\begin{array}{rcl} p(2) & = & 8 a_3 + 4 a_2 + 2 a_1 + a_0 = p(0) = a_0 \\ \Rightarrow & & 8 a_3 + 4 a_2 + 2 a_1 = 0 \\ \Rightarrow & & 4 a_3 + 2 a_2 + a_1 = 0 \\ \end{array}$$ and $$p^{\ \prime}(1) = 3 a_3 + 2 a_2 + a_1 = 0$$ gives us the homogeneous linear system of equations $$\begin{array}{rcl} 4 a_3 + 2 a_2 + a_1 & = & 0 \\ 3 a_3 + 2 a_2 + a_1 & = & 0 \\ \end{array}$$ whose augmented matrix reduces to $$\left[ \begin{array}{cccc} 4 & 2 & 1 & 0 \\ 3 & 2 & 1 & 0 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & \frac{1}{2} & 0 \\ \end{array} \right]$$ $\Rightarrow p(t) = a_3 t^3 + a_2 t^2 + a_1 t + a_0$ has coefficients satisfying the equations $a_3 = 0$ and $a_2 = -\frac{1}{2} a_1.$ Thus $$\begin{array}{rcl} p(t) & = & a_3 t^3 + a_2 t^2 + a_1 t + a_0 \\ & = & 0 \cdot t^3 -\frac{1}{2} a_1 t^2 + a_1 t + a_0 \\ & = & a_1 \left(-\frac{1}{2} t^2 + t \right) + a_0 (1) \\ \end{array}$$ So $$V = \left\{ \ a_1 \left( -\frac{1}{2} t^2 + t \right) + a_0 (1) \ \middle\vert \ a_1 , a_0 \in \mathbb{R} \ \right\} = \textrm{Span}\left\{ -\frac{1}{2} t^2 + t \ , \ 1 \right\}.$$
• Homework: For each of the following, find a spanning set $S.$
  • 1. $V = \left\{ y \ \middle\vert \ y^{\ \prime \prime} - 4 y = 0 \textrm{ and } y(0) = 0 \ \right\}.$
    2. $V = \left\{ y \ \middle\vert \ y^{\ \prime \prime} - 4 y = 0 \textrm{ and } y^{\ \prime}(0) = 0 \ \right\}.$
    3. $V = \left\{ y \ \middle\vert \ y^{\ \prime \prime} + y = 0 \textrm{ and } y \left(\frac{\pi}{4}\right) = 0 \ \right\}.$
    4. $V = \left\{ p \in \mathcal{P}_5 \ \middle\vert \ p(1) = 0 \textrm{ and } p(-1) = 0 \right\}.$
    5. $V = \left\{ p \in \mathcal{P}_2 \ \middle\vert \ p^{\ \prime}(1) = 0 \right\}.$
    6. $V = \left\{ p \in \mathcal{P}_4 \ \middle\vert \ p^{\ \prime}(1) = 0 \textrm{ and } p(-2) = 0 \right\}.$
    7. $$V = \left\{ A \in M_2(\mathbb{R}) \ \middle\vert \ A \left[ \begin{array}{c} 1 \\ -2 \\ \end{array} \right] = \vec{0} \right\}.$$
    8. $$V = \left\{ A \in M_3(\mathbb{R}) \ \middle\vert \ A \left[ \begin{array}{cc} 1 & 1 \\ -1 & 0 \\ 0 & -1 \\ \end{array} \right] = \left[ \begin{array}{cc} \vec{0} & \vec{0} \\ \end{array} \right] \right\}.$$