Vectors and Matrices


1. Complex Numbers

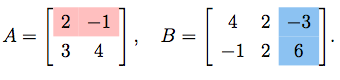
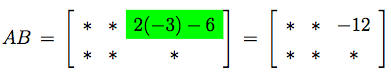
A Complex Number is an expression written in the form $z = \alpha + \beta i$ where $\alpha , \beta$ are real, and $i = \sqrt{-1}$ is a formal symbol satisfying the relation $i^{\, 2} = -1.$ We call $\alpha = \text{Re} \, z$ the real part and $\beta = \text{Im} \, z$ the imaginary part of $z = \alpha + \beta i.$ So a real number $\alpha$ is simply a complex number with zero imaginary part, thus embedding $\mathbb{R}$ as a subset of $\mathbb{C}.$ Formally, therefore, $\mathbb{C} = \mathbb{R} + \mathbb{R} \, i.$

The Complex Numbers are the set $$ \mathbb{C} = \left\{ \alpha + \beta i \, \vert \, \alpha , \beta \in \mathbb{R} \right\} $$ where $i^{\, 2} = -1.$ Let $z = x + y i$ and $\omega = u + v i \in \mathbb{C},$ then the complex numbers have the following properties:

Such properties are useful in simple computations with complex numbers, for instance:

Problem: Express the quotient $\displaystyle{\frac{z_1}{z_2}}$ in the form $\alpha+\beta i$ when $$z_1 \ = \ 4 + 3 i,\qquad z_2 \ = \ 1 + 2 i.$$ Solution: We use the fact that $$ \frac{z_1}{z_2} \ = \ \frac{z_1 \overline{z_2}}{z_2 \overline{z_2}},$$ so the denominator is now a real number. Then $$\eqalign{\frac{z_1}{z_2} \ & = \ \frac{(4+3i)(1-2i)}{(1+2i)(1-2i)} \\ & = \ \frac{(4+3i)(1-2i)}{1^2 + 2^2} \\ & = \ \frac{10 -5i}{5} \\ & = \ 2 -i.}$$

Problem: Write the expression $\displaystyle{\frac{z_1}{z_2} - \frac{z_1}{\overline{z_2}}}$ in the form $\alpha+\beta i$ when $$z_1 \ = \ 2-i,\qquad z_2 \ = \ 1 + 2 i.$$ Solution: We use the fact that $$ \frac{z_1}{z_2} - \frac{z_1}{\overline{z_2}} \ = \ \frac{z_1 \overline{z_2} - z_1 z_2}{z_2 \overline{z_2}},$$ so the denominator is now a real number. When $z_1 = 2-i,\ \ z_2 = 1 + 2 i,$ we have $$z_1 \overline{z_2} - z_1z_2 \ = \ -4 - 8i,$$ while $$ z_2 \overline{z_2} \ = \ (1+2i)(1-2i) \ = \ 5.$$ Thus $$ {\frac{z_1}{z_2} - \frac{z_1}{\overline{z_2}}} \ = \ \frac{-4 - 8i}{5}\ = \ -\frac{4}{5} - \frac{8}{5}i.$$

2. Vectors

A Vector is an ordered $n$-tuple of real numbers, a list ordered downwards, and written as a column: $$ \ \ {\bf v} = \left[\begin{array}{cc} v_1 \\ v_2 \\ \vdots \\ v_{n} \end{array}\right]. $$ The entries of ${\bf v}$ are its components, and $v_j$ is called the $j^{th}$-component. The set of all such $n$-component vectors will be denoted by $\mathbb{R}^n$ - often called Euclidean $n$-space. Just as we realize Euclidean $1$-space as the number line, Euclidean $2$-space as the set of all ordered pairs $(a, b)$, and $3$-space as the set of all ordered triples $(a,b, c),$ thus we will often realize $\mathbb{R}^n$ as the set of all ordered $n$-tuples $(a_1, a_2, \ldots, a_{n})$ of real numbers. Then we can think and speak of a point $(a_1, a_2, \ldots, a_{n})$ as corresponding to the vector ${\bf a}$ whose components are $a_1, a_2, \ldots, a_{n}$ and vice versa.

Euclidean $n$-space is the set $$\mathbb{R}^n = \left\{ \ \left[ \begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_n \\ \end{array} \right] \ \ \middle\vert \ \ v_1 , v_2 , \dots , v_n \in \mathbb{R} \right\},$$ which may sometimes be represented as $$\left\{ (v_1 , v_2 , \dots , v_n) \ \middle\vert \ v_1 , v_2 , \dots , v_n \in \mathbb{R} \right\}.$$

The definitions of vector addition and scalar multiplication in $\mathbb{R}^2$ and $\mathbb{R}^3$ extend naturally:

We add vectors ${\bf u},\ {\bf v}$ in $\mathbb{R}^n$ by $${\bf u} + {\bf v} \ = \ \left[\begin{array}{c} u_1 \\ u_2 \\ \vdots \\ u_{n} \end{array} \right] + \left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_{n} \end{array} \right] \ = \ \left[\begin{array}{c} u_1 + v_1 \\ u_2 + v_2 \\ \vdots \\ u_{n} + v_{n} \end{array} \right],$$ and form the scalar multiple $k {\bf v}$ of $k$ in $\mathbb{R}$ and ${\bf v}$ in $\mathbb{R}^n$ by $$k {\bf v} \ = \ k \left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_{n} \end{array} \right] \ = \ \left[\begin{array}{c} kv_1 \\ kv_2 \\ \vdots \\ kv_{n} \end{array} \right].$$

In other words, calculations are done component-wise. For example, in $\mathbb{R}^4$ $$ 3{\bf u} - 5 {\bf v} \ = \ 3\left[\begin{array}{cc} 2 \\ -1 \\ 3\\ 7 \end{array} \right] -5 \left[\begin{array}{cc} 4 \\ -2 \\ 2 \\ 3 \end{array} \right] \ = \ \left[\begin{array}{cc} 6 \\ -3 \\ 9\\ 21 \end{array} \right] - \left[\begin{array}{cc} 20 \\ -10 \\ 10 \\ 15 \end{array} \right] \ = \ \left[\begin{array}{cc} -14 \\ 7 \\ -1 \\ 6 \end{array} \right].$$

General vectors in $\mathbb{R}^n$ have the properties:

Let ${\bf u}, {\bf v}, {\bf w} \in \mathbb{R}^n$ and $c, d \in \mathbb{R},$ then

The following operation will generalize to matrix multiplication.

The Dot Product of vectors $${\bf u}\ = \ \left[\begin{array}{c} u_1 \\ u_2 \\ \vdots \\ u_{n} \end{array} \right], \quad {\bf v} \ = \ \left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_{n} \end{array} \right] \ \in \mathbb{R}^n$$ is defined by $${\bf u} \cdot {\bf v} \ = \ u_1 v_1 + u_2 v_2 + \cdots + u_{n} v_{n}.$$

3. Matrices

An $m \times n$ Matrix with real entries is a set of $mn$ real numbers $a_{j , \, k} \, , 1 \le j\le m,\ 1 \le k \le n,$ listed either as an array with $m$ rows and $n$ columns or as a row of $n$ column vectors as shown in $$ A \ = \ \left[\begin{array}{cc} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3, n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m, 2} & a_{m,3} & \cdots & a_{m, n} \end{array}\right] \ = \ \big[\begin{array}{cc} {\bf a}_1 & {\bf a}_2 & \ldots & {\bf a}_{n}\\ \end{array}\big] $$ where $${\bf a}_1 = \left[\begin{array}{c} a_{1,1} \\ a_{2,1} \\ \vdots \\ a_{m,1} \end{array} \right], \quad {\bf a}_2 = \left[\begin{array}{c} a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m,1} \end{array} \right], \quad \ldots , \quad {\bf a}_{n} = \left[\begin{array}{c} a_{1,n} \\ a_{2, n} \\ \vdots \\ a_{m,n} \end{array} \right]$$ are column vectors in $\mathbb{R}^m$. These definitions will be used interchangeably. To keep from drowning in notation, however, it's common to write a matrix as $A = [a_{j, \, k}]$ instead of writing out all the entries in $A$. The set of all $m \times n$ matrices with real entries will be denoted by $M_{m \times n}(\mathbb{R})$.

The set of $m \times n$ Matrices is given by $$ M_{m \, \times \, n}(\mathbb{R}) = \left\{ \ \left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \\ \end{array} \right] \quad \middle\vert \quad \begin{array}{c} a_{\,i,\,j} \in \mathbb{R} \\ \textrm{for } i = 1, 2, \dots , m \\ \textrm{and } j = 1, 2, \dots , n \\ \end{array} \ \right\} $$ If $m = n,$ we use the notation $M_n(\mathbb{R})$ in place of $M_{n \times n}(\mathbb{R}).$

For each $n,$ there is a unique Identity Matrix in $M_n(\mathbb{R}).$ This is the matrix with $1$'s down the diagonal, and $0$'s otherwise. $$ I_n = \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{array} \right] $$ By $0_{m , \, n} \in M_{m \, \times \, n}(\mathbb{R})$ and $0_n \in M_n(\mathbb{R})$ we mean the appropriately sized matrix whose every entry is $0.$

Addition and scalar multiplication of matrices are defined as follows:

We add matrices $A, B \in M_{m \times n}(\mathbb{R})$ entry-by-entry: $$A + B \ = \ [a_{j , \, k}] + [b_{j , \, k}] \ = \ [a_{j , \, k} + b_{j , \, k}].$$ In particular, $A + B$ is defined only when both $A$ and $B$ are $m \times n,$ i.e., have the same shape, and then $A + B$ also has the same shape since it is $m \times n$. For example, $$\left[\begin{array}{ccc} 1 & 2 & 3 \\ -3 & 4 & -1 \\ \end{array}\right] + \left[\begin{array}{ccc} 4 & -1 & 1 \\ 2 & -4 & -1 \\ \end{array}\right]\ = \ \left[\begin{array}{ccc} 5 & 1 & 4 \\ -1 & 0 & -2 \\ \end{array}\right].$$ We define the scalar multiple of $k \in \mathbb{R}$ and $A \in M_{m \times n}(\mathbb{R})$ by $$k A \ = \ k [a_{j , \, k}] \ = \ [k a_{j , \, k}].$$ Thus each entry in $A$ is multipled by $k;$ in particular, the scalar multiple $k A$ of an $m \times n$ matrix $A$ also is $m \times n,$ so scalar multiplication preserves shape since the scalar multiple $k A$ is again $m \times n$. For example, $$3 \left[\begin{array}{cc} 1 & 2 & 3 \\ -3 & 4 & -1 \\ \end{array}\right]\ = \ \left[\begin{array}{cc} 3 & 6 & 9 \\ -9 & 12 & -3 \\ \end{array}\right].$$

Matrices have the same algebraic properties that vectors have. To introduce multiplication, let's begin with the product of a matrix and a vector:

The Product of a Matrix with a Vector is given by the following: Let $A=\big[{\bf a}_1\ {\bf a}_2 \ \ldots {\bf a}_{n} \big]$ be an $m \times n$ matrix written as $n$ column vectors $ {\bf a}_1, {\bf a}_2, \dots, {\bf a}_{n}$ in $\mathbb{R}^m$ and ${\bf x}$ a vector in $\mathbb{R}^n,$ then $A{\bf x}$ is the vector in ${\mathbb R}^m$ defined by $$A{\bf x} \ = \ \big[{\bf a}_1\ {\bf a}_2 \ \ldots {\bf a}_{n} \big] \left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_{n} \end{array} \right] \ = \ x_1 {\bf a}_1 + x_2 {\bf a}_2 + \ldots + x_{n} {\bf a}_{n}.$$ Thus the product of an $m \times n$ matrix $A$ and a vector ${\bf x}$ in $\mathbb{R}^n$ is a vector $A {\bf x}$ in $\mathbb{R}^m.$

Collecting all these concepts together we can solve:

Problem: Determine the vector $${\bf v} \ = \ \left[\begin{array}{cc} 2 & 1 \\ 4 & 2 \\ \end{array}\right] \left[\begin{array}{c} 2 \\ 3 \\ \end{array}\right] - 5 \left[\begin{array}{c} 1 \\ 3 \\ \end{array}\right]$$ in $\mathbb{R}^2$.
Solution: Using the properties of matrices above, 		$$ \left[\begin{array}{cc} 2 & 1 \\ 4 & 2 \\ \end{array}\right] \left[\begin{array}{c} 2 \\ 3 \\ \end{array}\right] \ = \ 2 \left[\begin{array}{c} 2 \\ 4 \\ \end{array}\right] + 3 \left[\begin{array}{c} 1 \\ 2 \\ \end{array}\right] \ = \ \left[\begin{array}{c} 7 \\ 14 \\ \end{array}\right].$$ So $${\bf v} \ = \ \left[\begin{array}{c} 7 \\ 14 \\ \end{array}\right] - 5 \left[\begin{array}{c} 1 \\ 3 \\ \end{array}\right] \ = \ \left[\begin{array}{c} 2 \\ -1 \\ \end{array}\right].$$

We can multiply two matrices if they have the appropriate relative sizes. Namely, we can multiply matrices $A$ and $B$ if the number of columns of $A$ equals the number of rows of $B.$

The Product of Two Matrices is given by the following: Let $A = \left[ a_{i , \, j} \right]$ be an $m \times p$ matrix and $B = \left[ b_{i , \, j} \right]$ be a $p \times n$ matrix, then the product $A B$ is the $m \times n$ matrix whose $(i,j)^{th}$-entry is the dot product of the $i^{th}$ row of $A$ with the $j^{th}$ column of $B.$ If we denote $A B = \left[ c_{i , \, j} \right],$ then $$ c_{i , \, j} = a_{i , \, 1} b_{1 , \, j} + a_{i , \, 2} b_{2 , \, j} + \cdots + a_{i , \, p} b_{p , \, j} = \sum_{k = 1}^p a_{i , \, k} b_{k , \, j}. $$

For example,

Suppose we wish to calculate the $(1,3)$-entry in the product $AB$ of the matrices

We will need to take the dot product of the ${\bf r}_1$ row of $A$, highlighted in pink, with the ${\bf a}_3$ column of $B$, highlighted in blue. Then, as highlighted in green, the $(1,3)$-entry in the matrix product $AB$ is given by

The remaining entries can now be computed in the same way, showing that the matrix product $A B$ is the $2 \times 3$ matrix $$ \left[\begin{array}{cc} 2 & -1 \\ 3 & 4 \\ \end{array}\right] \left[\begin{array}{cc} 4 & 2 & -3 \\ -1 & 2 & 6 \end{array} \right] \ = \ \left[\begin{array}{cc} 9 & 2 & -12 \\ 8 & 14 & 15 \\ \end{array} \right].$$

Many of the familiar multiplicative properties of real numbers carry over to matrix multiplication.

Let $A, B,$ and $C,$ be matrices whose sizes allow the following operations to be performed, and $k \in \mathbb{R},$ then

But some multiplicative properties of real numbers do not carry over to matrices:

Failure of Commutativity:
The equality $AB = BA$ need not always hold for matrices $A, B.$ For example, $$ AB \ = \ \left[\begin{array}{cc} 0 & 1 \\ 0 & 2 \\ \end{array}\right] \left[\begin{array}{cc} 0 & 2 \\ 0 & 1 \\ \end{array}\right] \ = \ \left[\begin{array}{cc} 0 & 1 \\ 0 & 2 \\ \end{array}\right],$$ while $$ BA \ = \ \left[\begin{array}{cc} 0 & 2 \\ 0 & 1 \\ \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 2 \\ \end{array}\right] \ = \ \left[\begin{array}{cc} 0 & 4 \\ 0 & 2 \\ \end{array}\right].$$ 		Existence of Zero Divisors:
There are matrices $A$ and $B$ such that $AB = 0$ but neither $A$ nor $B$ is $0$ (i.e. the zero matrix). For example, when $$ A \ = \ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \\ \end{array}\right], \quad B\ = \ \left[\begin{array}{cc} 0 & 2 \\ 0 & 0 \\ \end{array}\right],$$ then $$ AB \ = \ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} 0 & 2 \\ 0 & 0 \\ \end{array}\right] \ = \ \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array}\right].$$