Compare

with
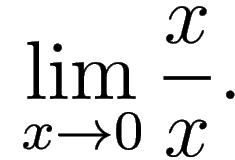
Note that in both cases we
have
 indeterminate forms
indeterminate forms.
The second limit is 1, since
In other words, the zero term
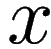
gets canceled and the
limit perfectly exists as a finite number.
To apply the same idea to

we first factor the bottom and then cancel the
zero term
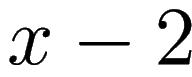
:
We first note that we can
not use the
Direct Substitution Property to evaluate
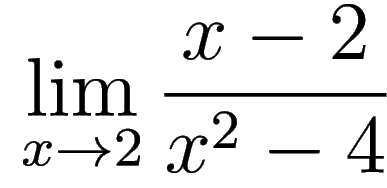
,
since the denominator
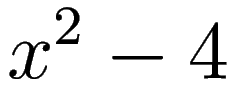
is 0 at
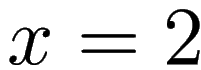
. In other words,
2 is not from the
domain of
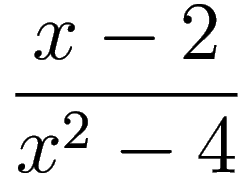
,
therefore
DSP can not be used. However, this does
not necessarily mean that the limit does not exist. Actually, this limit does exist.
To understand it, we first note that the problem of finding the
limit
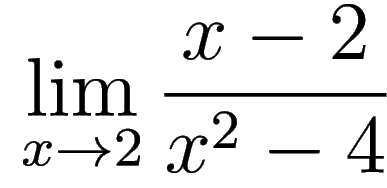
is different from
the problem of evaluating
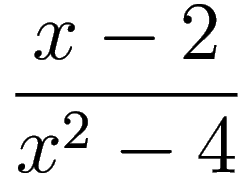
at
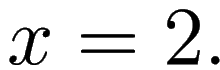
The latter is
impossible, since we can't divide by 0. Nevertheless, the limit of
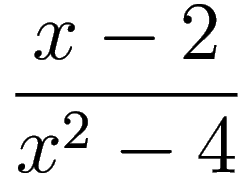
when

is goes to 2 does exist. Indeed, by
the nature of a limit when we are evaluating
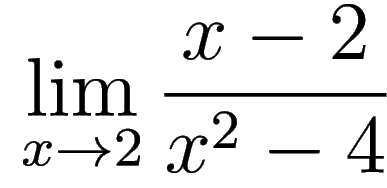
we are basically trying to see what
happens to
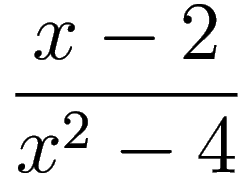
when

is close to 2 (as
close to 2 as we like), but
not equal to 2 (see
Definition of limit). One can check that
if
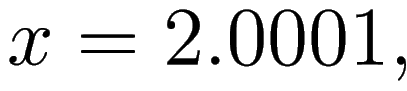
then
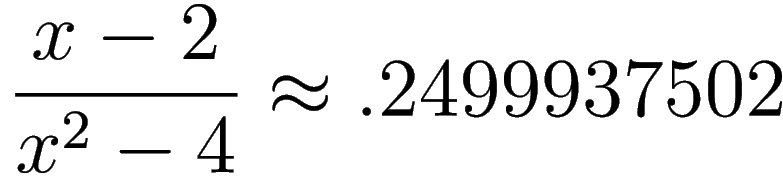
if
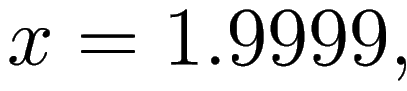
then
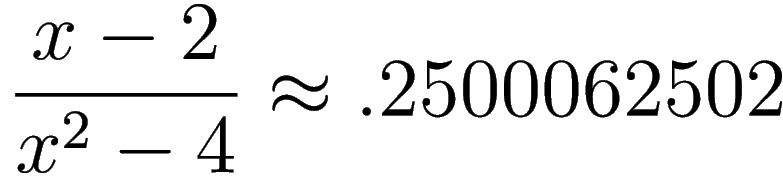
Both are very close to
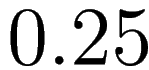
(which is

). This suggests
that
However, our goal here is to prove it rigorously using the
Limit Laws. To this end, we note that the
numerator of
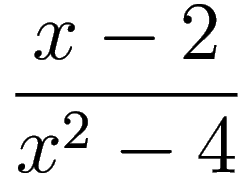
is also 0
when
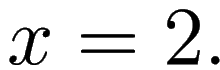
In other
words, when

approaches 2, the top and the bottom of
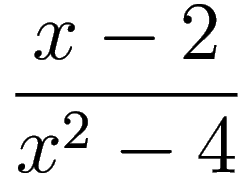
go to zero.
In this case we say that the limit is a
 indeterminate form
indeterminate form. To evaluate this
limit, we note that since
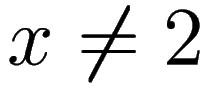
(as we
discussed before), then, by algebra, we have
STEP A1: We show that
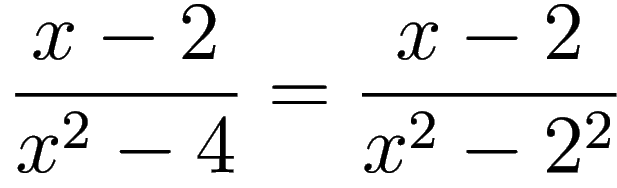
.
WORK: By
arithmetic 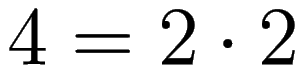
and

(by
definition of
second power). Therefore
hence
STEP A2: We show that
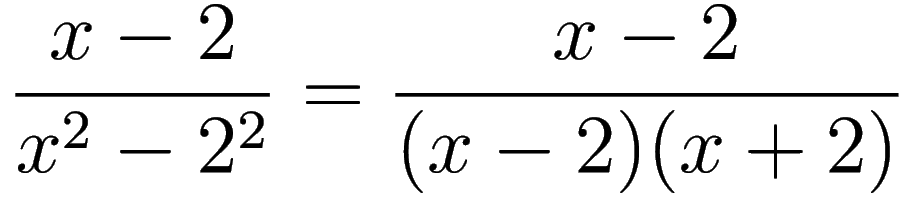
.
WORK: Here we use the
identity
In our case

and
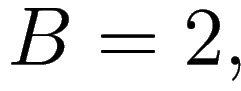
therefore
hence
STEP A3: We show that
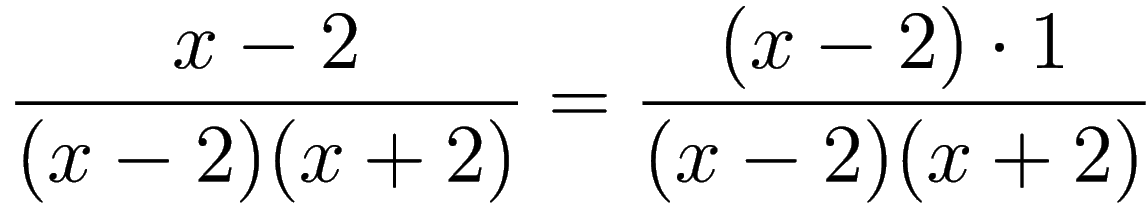
.
WORK: Multiplication by
1 does not change the expression.
Therefore
hence
STEP A4: We show that
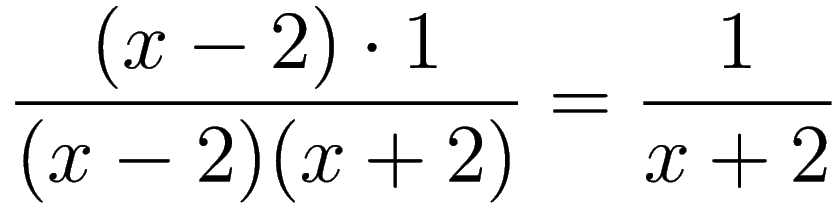
.
WORK: We have
In our case
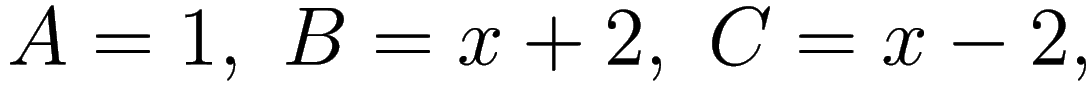
therefore
So, we conclude that
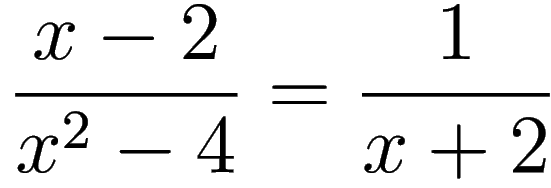
if

therefore
and now we can use the
Direct Substitution Property to find
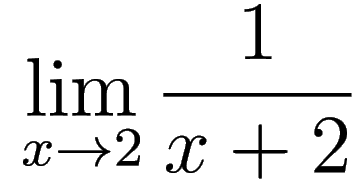
. We have
hence
Solution (full): We first note that
is

type of an indeterminate form.
Indeed, the top and the bottom of
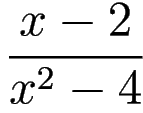
go to 0 when
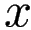
goes to 2:
when

.
Therefore we
can't use
the
Direct Substitution Property. Instead, we do the following: