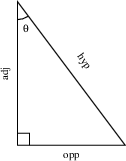
First let's define the six trig functions: sine, cosine, tangent, secant, cotangent and cosecant, and see what they have to do with triangles. The mnemonic SOH-CAH-TOA captures the definitions of the three most common trig functions, at least for angles between 0 and $\pi/2$ radians (90 degrees).
| $$\text{Sine }=\frac{\text{Opposite}}{\text{Hypotenuse}}$$ $$\displaystyle \text{Cosine }= \frac{\text{Adjacent}}{\text{Hypotenuse}}$$ $$\displaystyle \text{Tangent }= \frac{\text{Opposite}}{\text{Adjacent}}$$ |

|
The other trig functions are defined in terms of first three:
| $$\text{Secant }= \frac{1}{\text{Cosine}} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$$ $$\text{Cosecant }= \frac{1}{\text{Sine}} = \frac{\text{Hypotenuse}}{\text{Opposite}}$$ $$\text{Cotangent }= \frac{1}{\text{Tangent}} = \frac{\text{Adjacent}}{\text{Opposite}}$$ |
|
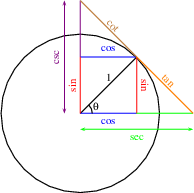
Below is how to find them in the unit circle.