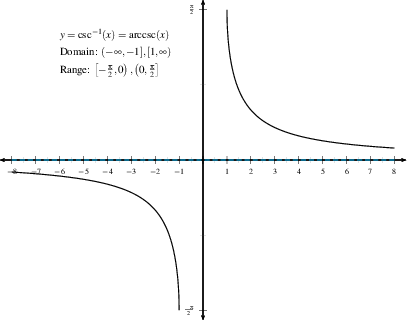Inverse Trig Functions

Sine, Cosine, and Tangent

The functions sine, cosine and tangent are not one-to-one, since they repeat (the first two every $2\pi$, the latter every $\pi$). To get inverse functions, we must restrict their domains. We could do this in many ways, but the convention is:

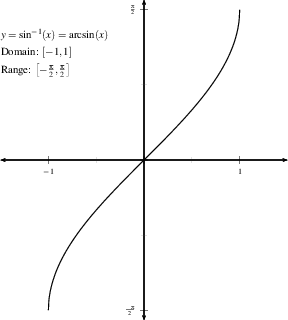
• For sine, we restrict the domain to $[-\pi/2, \pi/2]$. By definition, $\sin^{-1}(x)$ is the angle between $-\pi/2$ and $\pi/2$ whose sine is $x$. This only makes sense if $-1 \le x \le 1$. In other words,

  $$\theta = \sin^{-1}(x) \quad \Longleftrightarrow \quad \sin(\theta)=x, \quad \hbox{ for }-\pi/2 \le \theta \le \pi/2.$$

  
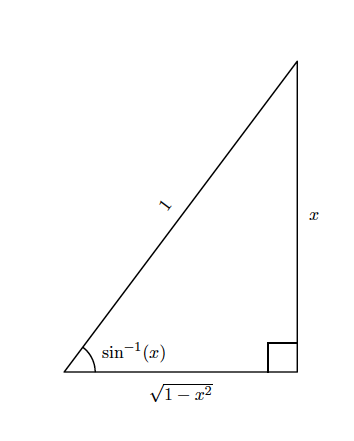
  The best way to understand $\sin^{-1}(x)$ is to draw a right triangle with sides of length $x$ and $\sqrt{1-x^2}$ and hypotenuse of length $1$.


• For cosine, we restrict the domain to $[0,\pi]$. By definition, $\cos^{-1}(x)$ is the angle between $-\pi/2$ and $\pi/2$ whose cosine is $x$. So,

  $$\theta = \cos^{-1}(x) \quad \Longleftrightarrow \quad \cos(\theta)=x, \quad \hbox{ for }0 \le \theta \le \pi.$$

  
  



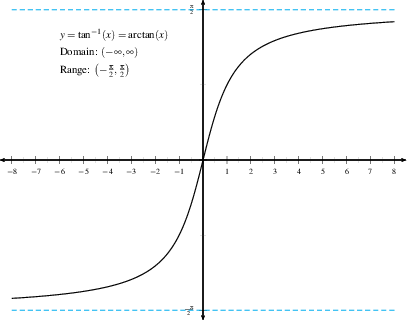
• For tangent, we restrict the domain to $(-\pi/2, \pi/2)$.

  $$\theta=\tan^{-1}(x) \quad \Longleftrightarrow \quad \tan(\theta)=x, \quad \hbox{ for } -\pi/2 < \theta < \pi/2.$$

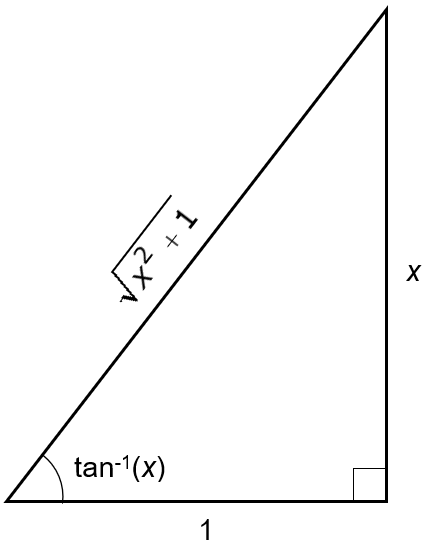
  This is defined for all real values of $x$. To understand $\tan^{-1}(x)$, draw a right triangle where the legs have length $x$ and $1$ and the hypotenuse has length $\sqrt{1+x^2}$.
  
  

Other Trig Functions

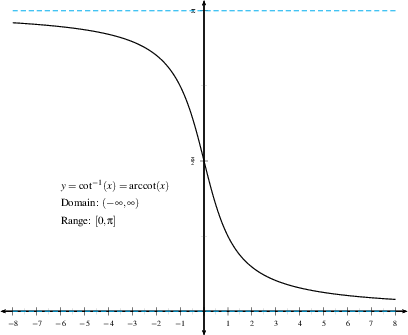
Since $\cot(\theta)=1/\tan(\theta)$, $\cot^{-1}(x)=\tan^{-1}(1/x)$.

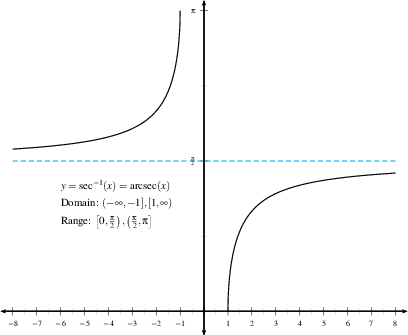
Likewise, $\sec^{-1}(x)=\cos^{-1}(1/x)$ and $\csc^{-1}(x)=\sin^{-1}(1/x)$. So, they can be derived from the inverse functions defined above.

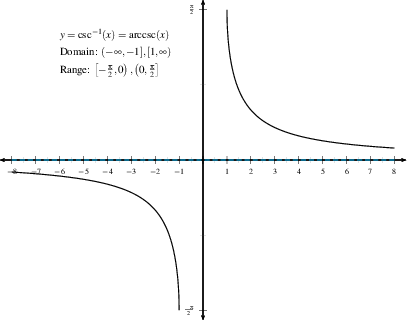
Some Facts:

• The function $\cos^{-1}$ is closely related to $\sin^{-1}$. Specifically, $\cos^{-1}(x) = \frac{\pi}{2}-\sin^{-1}(x)$. This is because $\cos\left(\frac{\pi}{2}-\theta\right)=\sin(\theta)$.


• In practice, $\sin^{-1}$ and $\tan^{-1}$ come up a lot, $\cos^{-1}$ and $\sec^{-1}$ come up occasionally, while $\cot^{-1}$ and $\csc^{-1}$ almost never come up.


• Another name for $\sin^{-1}(x)$ is $\arcsin(x)$. (But watch out: Some authors use $\arcsin(x)$ to mean any angle whose sine is $x$, not just the angle between $-\pi/2$ and $\pi/2$.) Likewise, $\arctan(x)$ and $\arccos(x)$ mean $\tan^{-1}(x)$ and $\cos^{-1}(x)$.


• The notation $\sin^{-1}(x)$ should not be confused with expressions like $\sin^2(x)$. $\sin^2(x)$ is shorthand for $(\sin(x))^2$, but $\sin^{-1}(x)$ is not $\sin(x)^{-1}$. It is the inverse sine of $x$. The same applies to $\cos^{-1}(x)$ and $\tan^{-1}(x)$. These are inverse functions, not reciprocals!