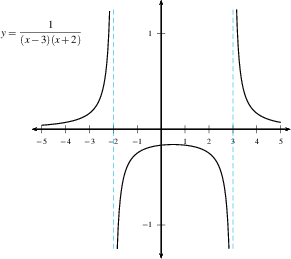
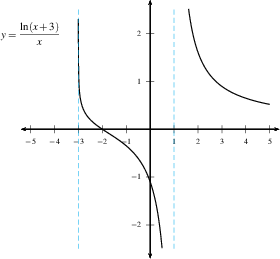
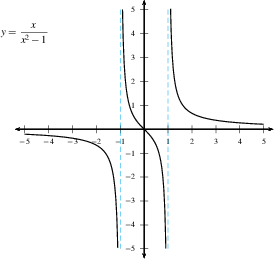
The statement $$\lim_{x \to a}
f(x) = \infty$$ means "whenever $x$ is close to (but not equal to)
$a$, then $f(x)$ is a large positive number. In other words,
as $x$ gets closer and closer to $a$, $f(x)$ gets bigger and bigger
without bound. Likewise, the statement $$\lim_{x \to a} f(x) =
-\infty$$ means that "whenever $x$ is close to $a$, $f(x)$ is a large
negative number." Remember that $\infty$ is not a number!!
The word "infinity" literally means without
end. If a limit is $+ \infty$, then the function grows
without end. If the limit is $-\infty$, it shrinks without end.
|
Definition: The line $x=a$ is called a vertical asymptote of a function $f$ if at least one of the following is true:
|
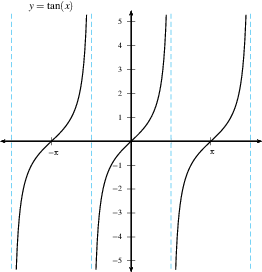
Here are some examples of graphs with a vertical asymptote.
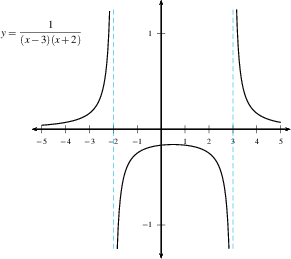

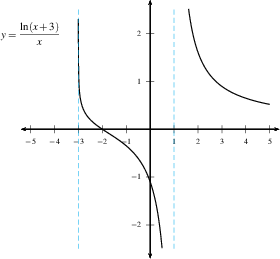
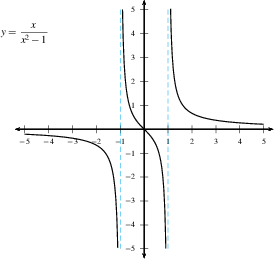
Rational functions often have vertical asymptotes when the denominator goes to zero (and the numerator doesn't), such as $f(x) =\dfrac{3}{x-4}$ or $f(x)=\dfrac{x^2-1}{x^2-4}$.