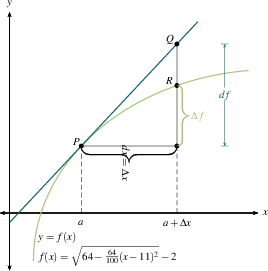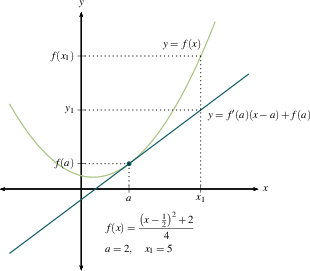
Derivatives can be used to get very good linear approximations to functions. By definition, $$f'(a) = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}.$$ In particular, whenever $x$ is close to $a$, $\frac{f(x)-f(a)}{x-a}$ is close to $f'(a)$. So whenever $x$ is close to $a$, $f(x) - f(a)$ is close to $f'(a) (x-a)$. This means that $$f(x) \approx f(a) + f'(a) (x-a)$$ whenever $x$ is close to $a$.
The function $L(x) = f(a) + f'(a) (x-a)$ is called the linearization of $f(x)$. The line $y=L(x)$ goes through $\big(a, f(a)\big)$ with slope $f'(a)$, so it is the line tangent to $y=f(x)$ at $\big(a, f(a)\big)$.
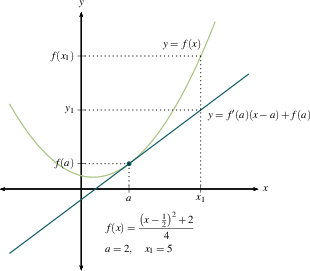
Differentials are another name for the same idea.
Let $\Delta x = x-a$ be the change in $x$, and $\Delta f = f(x) - f(a)$ be the change in $f$.
And let $dx=x-a$, and let $df= f'(a) dx$.
Our approximation is then $$\Delta f \approx df.$$
The actual changes $\Delta f$ and $\Delta x$ are the rise and run
along the secant line between $P=\big(a, f(a)\big)$ and $R=\big(x, f(x)\big)$.
The differentials $df$ and $dx$ are the rise and run along the
tangent line as we go from $a$ to $x$.