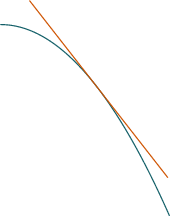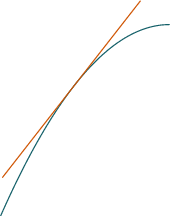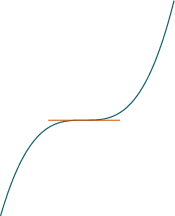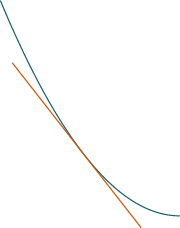Concavity, Points of Inflection, and the Second Derivative Test
Concavity and Points of Inflection
Definitions:
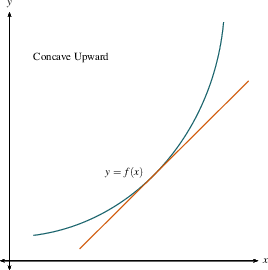 
 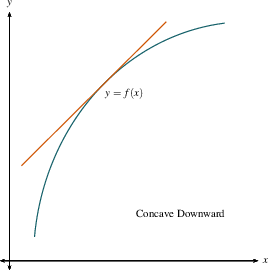
- If the graph of $f$ lies above all of its
tangent lines on an open interval, the we say
it is concave up on that interval.
-
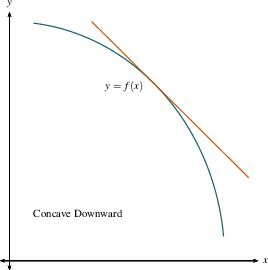
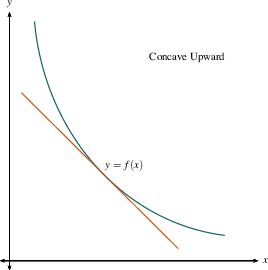
If the graph of $f$ lies below all of its
tangent lines on an open interval, then we say
it is concave down on that interval.
-
A point, $P$, on a continuous curve $f(x)$ is
an inflection point if $f$ changes
concavity there.
|
When a curve is concave up, it is sort of bowl-shaped, and
you can think it might hold water. When it is concave down, it
is sort of upside-down-bowl-like, and water would run off of it.
How-to
The intervals of concavity can be found in the same way used to determine the intervals of
increase/decrease, except that we use the second derivative instead of the first. In particular, since $(f')'=f''$, the intervals of increase/decrease for the first derivative will determine the concavity of $f$:



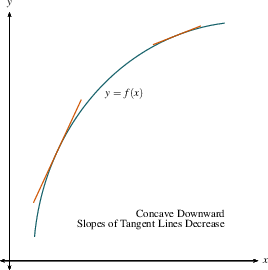
- If possible, factor $f''$.
If $f''$ is a quotient, factor the numerator and denominator (separately).
- Find all critical numbers $x=s$ of $f'$. These are the points
where $(f')'=0$ or $(f')'$ doesn't exist (i.e., the points where $f''=0$ or where $f''$ doesn't exist).
- Draw a number line with tick marks at each critical number $s$.
- For each interval in which the function $f$ is defined, find the sign of the second derivative $f''$.
- If $f''(b) \gt 0$, then $f'$
is increasing on the interval containing $b$. This means that the slopes are
increasing, so $f$ is concave up. Draw a right-side-up
bowl over that interval on your number line. Similarly, if
$f''(b) \lt 0$, draw an upside-down bowl.
- That's it! You can now
see the intervals where $f$ is concave up or down.
|
The Second Derivative Test
Theorem:
-
If $f''(x)>0$ for all $x$ in an open interval,
then it is concave up on that interval.
-
If $f ''(x) < 0$ for all $x$ in an open interval, then it is concave
down on that interval.
|
Second Derivative Test:
-
If $f'(c)=0$ and $f''(c) \gt0$, then there is a
local minimum at $x=c$.
- If $f'(c)=0$ and $f''(c) \lt 0$, then there is a local maximum at
$x=c$.
- If $f'(c)=0$ and $f''(c)=0$, or if $f''(c)$ doesn't exist, then
the test is inconclusive. There might be a local maximum or minimum, or
there might be a point of inflection.
|
The reasoning behind the test is simple: if $f''(c) \gt 0$, then
$f'(x)$ is increasing near $x=c$. Since $f'(c)=0$, this means that
$f'(x)$ used to be negative and is about to be positive. So the
curve bottoms out at $x=c$ and then heads back up. The critical number
$x=c$ is the bottom
of the concave-up bowl. Likewise, if $f''(c) \lt 0$ and $f'(c)=0$, then
$f'(x)$ is decreasing; it used to be positive and is about to be
negative. The point $x=c$ is at the top of an upside-down bowl.
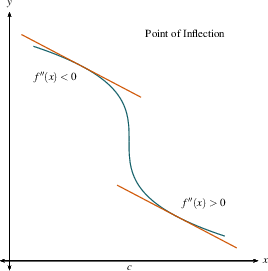
Inflection Points
An inflection point is a point where concavity changes sign from plus to minus or from minus to plus.

Example: Find the concavity of $f(x) = x^3 - 3x^2$.
Solution:
Since $f'(x)=3x^2-6x=3x(x-2)$,our two critical points for $f$ are at $x=0$ and $x=2$. Meanwhile, $f''(x)=6x-6$,
so the only critical point for $f'$ is at $x=1$. It's easy to see that
$f''$ is negative for $x \lt 1$ and positive for $x \gt 1$, so our curve
is concave down for $x \lt 1$ and concave up for $x \gt 1$, and
there is a point of inflection at $x=1$.
As for the critical points, $f''(0)=-6 \lt 0$, so we have a local
maximum at $x=0$. $f''(2)=6 > 0$, so we have a local minimum at
$x=2$. These results agree with what we got from the first derivative
test.
|
Visual Wrap-up
| $f'< 0$ | $f'=0$ | $f'> 0 $ |
| $f''<0$ | 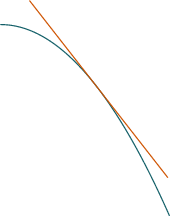 | 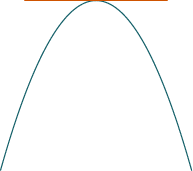 | 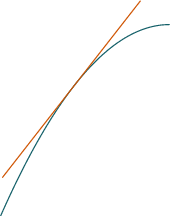 |
| $f''=0$ | 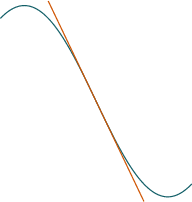 | 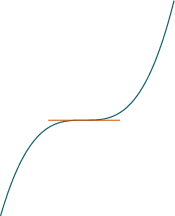 | 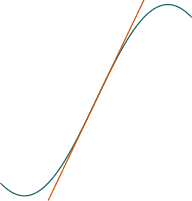 |
| $f''>0$ | 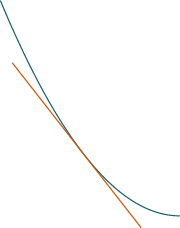 |  | 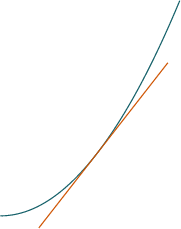 |