The First Derivative Test


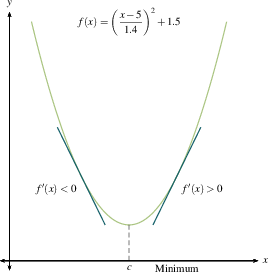
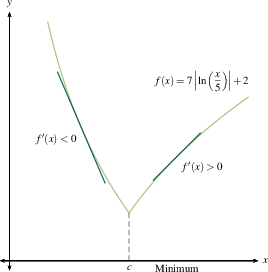
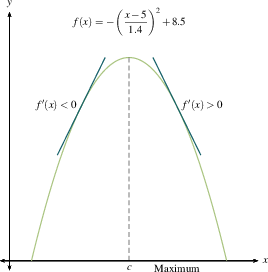
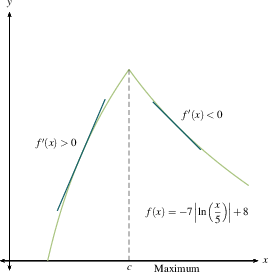
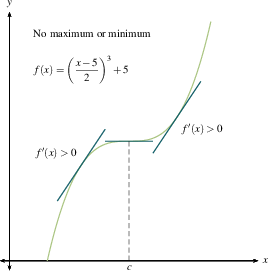
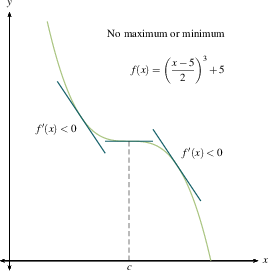
Remember that critical numbers are the only places where a function can have a local maximum or minimum (aside from endpoints), and are the only places where $f'(x)$ can change sign. These are related by


The First Derivative Test: Let $c$ be a critical number for a continuous function $f$
  1. If $f'(x)$ changes from positive to negative at $c$, then $f(c)$ is a local maximum.
  2. If $f'(x)$ changes from negative to positive at $c$, then $f(c)$ is a local minimum.
  3. If $f'(x)$ does not change sign at $c$, then $f(c)$ is neither a local maximum or minimum.





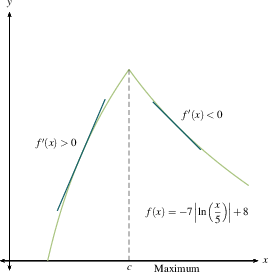
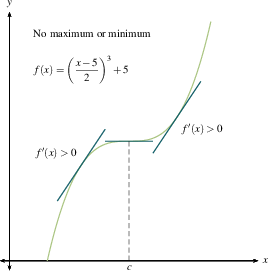
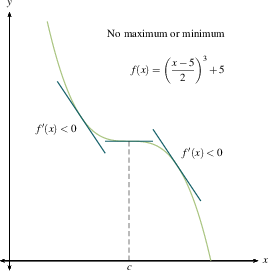
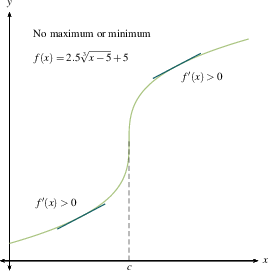
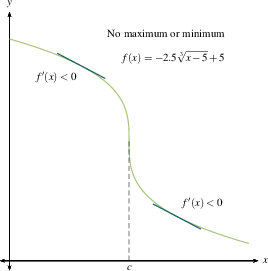
This should jibe with your common sense. A local maximum is where you stop going up and start coming down. A local minimum is where you stop going down and start coming up. If you flatten out and then resume going in the direction you were already heading, you're at a critical point but not at a maximum or minimum. Once you make a sign chart for $f'(x)$, as we outlined previously, then you know where all the local maxima and minima are.


Example: Find the maxima and minima of $f(x)=x^3-3x^2$.


Solution: We already determined that $f'(x)$ is positive on $(-\infty,0)$, negative on $(0,2)$ and positive on $(2,\infty)$. Since $f'$ goes from positive to negative at $x=0$, there is a local maximum at $x=0$. Since $f'$ goes from negative to positive at $x=2$, there is a local minimum at $x=2$.