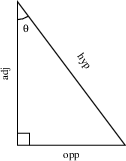
First let's define the six trig functions: sine, cosine, tangent, secant, cotangent and cosecant, and see what they have to do with triangles. The mnemonic SOH-CAH-TOA captures the definitions of the three most common trig functions, at least for angles in the first quadrant (between 0 and $\pi/2$ radians). You will need to know the following:
| $$\text{Sine }=\frac{\text{Opposite}}{\text{Hypotenuse}}$$ $$\displaystyle \text{Cosine }= \frac{\text{Adjacent}}{\text{Hypotenuse}}$$ $$\displaystyle \text{Tangent }= \frac{\text{Opposite}}{\text{Adjacent}}$$ | |
|
 |
The other trig functions are defined as reciprocals of the first
three, and below you will find the reciprocal relationships (which
you need to know) as well as the resulting triangle relationships
of the other three trig functions. You need not memorize the
triangle relationships of these trig functions, as long as you
know the reciprocal relationships. (The colorful diagram is
interesting, but you need not worry about it.)
| $$\text{Secant }= \frac{1}{\text{Cosine}} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$$ $$\text{Cosecant }= \frac{1}{\text{Sine}} = \frac{\text{Hypotenuse}}{\text{Opposite}}$$ $$\text{Cotangent }= \frac{1}{\text{Tangent}} = \frac{\text{Adjacent}}{\text{Opposite}}$$ |  |
This video will show how to find values of trig functions in the
unit circle.