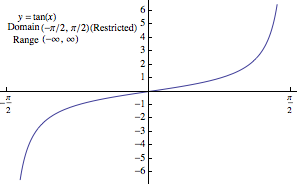Inverse Trig Functions
Sine and Tangent
The functions sine, tangent and secant are not one-to-one, since
they repeat (every $2\pi$ for sine and secant, and every $\pi$ for
tangent). To get inverse functions, we must restrict their
domains. We could do this in many ways, but the convention is:
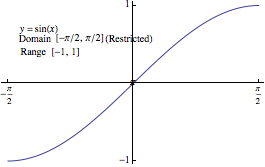
SINE: We restrict the domain to $[-\pi/2, \pi/2]$ to
ensure our function is one-to-one. By definition,
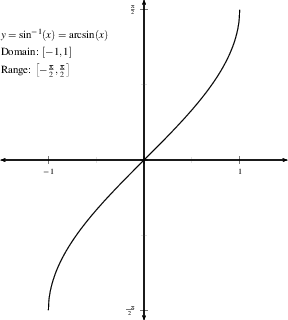
$\sin^{-1}(x)$ is the angle
in $[-\pi/2,\pi/2]$ whose sine is $x$. This only makes sense if $-1
\le x \le 1$.
| $$\theta = \sin^{-1}(x) \quad
\Longleftrightarrow \quad \sin(\theta)=x, \quad \hbox{ for
}-\pi/2 \le \theta \le \pi/2.$$ |
Examples: $\sin^{-1}(1/2)$ is the angle $\theta$ (in
the restricted domain) for which $\sin(\theta)=1/2$. Thus
$\theta=\pi/6$; i.e. $\sin^{-1}(1/2)=\pi/6$.
DO: Find $\sin^{-1}\left(\frac{\sqrt 3}{2}\right)$
TANGENT: We restrict the domain to
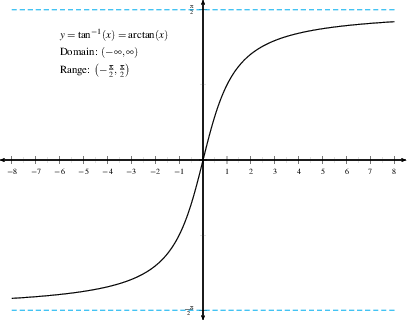
$(-\pi/2,\pi/2)$. By definition, $\tan^{-1}(x)$ is the angle in
$(-\pi/2,\pi/2)$ whose tangent value is $x$. Here, $x$ can be
any real number; can you see why?
| $$\theta=\tan^{-1}(x)
\quad \Longleftrightarrow \quad \tan(\theta)=x, \quad \hbox{
for } -\pi/2 < \theta < \pi/2.$$ |
DO:
Find $\tan^{-1}(\sqrt 3)$.
Some Facts
- In practice, $\sin^{-1}$ and $\tan^{-1}$ come up a lot,
$\sec^{-1}$ comes up occasionally, while $\cos^{-1}$,
$\cot^{-1}$ and $\csc^{-1}$ almost never come up.
- Another name for $\sin^{-1}(x)$ is $\arcsin(x)$.
Likewise, $\arctan(x)$ and $\arccos(x)$ mean $\tan^{-1}(x)$ and
$\cos^{-1}(x)$.
- The "exponent" $-1$ has more than one meaning, which you must
infer from the context. The notation $\sin^{-1}(x)$ should
not be confused with expressions like $\sin^2(x)$.
$\sin^2(x)$ is shorthand for $(\sin(x))^2$, but $\sin^{-1}(x)$
is not $\sin(x)^{-1}$. It is the inverse sine of $x$. The
same applies to $\cos^{-1}(x)$ and $\tan^{-1}(x)$.
Similarly, $f^{-1}(x)$ is the inverse of $f$, not
$1/f(x)$. These are inverse functions, not reciprocals.
Advanced play for those who are interested
The function $\cos^{-1}$ is closely related to $\sin^{-1}$.
Specifically, $\cos^{-1}(x) =
\frac{\pi}{2}-\sin^{-1}(x)$. This is because
$\cos\left(\frac{\pi}{2}-\theta\right)=\sin(\theta)$.
Similarly, since $\cot(\theta)=1/\tan(\theta)$,
$\cot^{-1}(x)=\tan^{-1}(1/x)$.
Likewise, $\sec^{-1}(x)=\cos^{-1}(1/x)$
DO: Carefully play with these statements and see if
you can see why they are true.