Logarithms as Inverse Exponentials
Throughout suppose that $a>1$. The function $y=\log_a(x)$ is
the inverse of the function $y=a^x$. In other words,
| $$\log_a(a^x) = x \qquad \hbox{and}
\qquad a^{\log_a(x)}=x$$ |
whenever these make sense.
The value of $\log_b(a)$ is the power
you raise $b$ to to get $a$.
Examples:
- Since $10^3=1000$, $\log_{10}(1000)=3$.
- Since $2^{-3}=1/8$, $\log_2(1/8)=-3$.
- $10^{\log_{10}(17)}=17$ and $2^{\log_2(.038)}=.038$
- Since $a^0=1$, no matter what $a$ is, $\log_a(1)=0$. In
general $\log_a(x)$ will be positive for $x>1$ and negative
for $x<1$.
- The domain of $a^x$ is $(-\infty, \infty)$, so the range of
$\log_a(x)$ is $(-\infty,\infty)$.
- The range of $a^x$ is $(0,\infty)$, so the domain of
$\log_a(x)$ is $(0,\infty)$. We cannot take the log of zero
or the log of a negative number.
Laws of Logarithms
The laws of logs follow from the law of exponents. You should know these.
Provided that $x>0$ and $y>0$ we have:
Logarithm Laws
- $\log_{a}(xy) = \log_a(x) + \log_a(y)$
- $\log_a(x/y) = \log_a(x) - \log_a(y)$
- $\log_a(x^r) = r \log_a(x)$
- $\log_b(a) = \frac{\log_x(a)}{\log_x(b)}$ for any
valid log base $x$
|
The last item above is the "change of base" formula, which helps in
approximating the value of logs using your calculator (which usually
has only $\ln x$ and $\log x$ which are logs with base $e$ and $10$
respectively). So $\log_7(5)=\frac{\ln 5}{\ln
7}=\frac{\log 5}{\log 7}$, either of which you can compute using
your calculator. These ratios are equal -- do not
think that $\ln 5=\log 5$! The power you raise $e$ to to get 5
is not the same as the power you raise $10$ to to get 5.
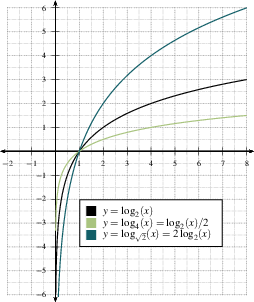
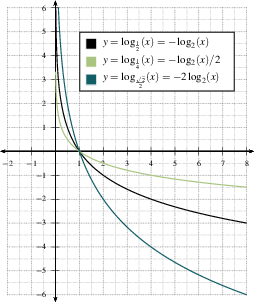
Graphs
Below are the graphs of the log functions when $a>1$ or $0
< a<1$.