Infinite Limits

The statement $$\lim_{x \to a} f(x) = \infty$$ tells us that whenever $x$ is close to (but not equal to) $a$, $f(x)$ is a large positive number.  A limit with a value of $\infty$ means that as $x$ gets closer and closer to $a$, $f(x)$ gets bigger and bigger; it increases without bound. Likewise, the statement $$\lim_{x \to a} f(x) = -\infty$$ tells us that whenever $x$ is close to $a$, $f(x)$ is a large negative number, and as $x$ gets closer and closer to $a$, the value of $f(x)$ decreases without bound. 

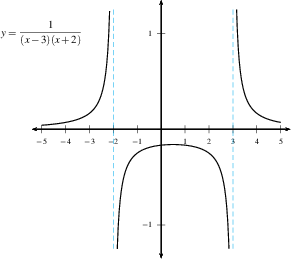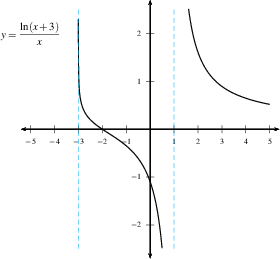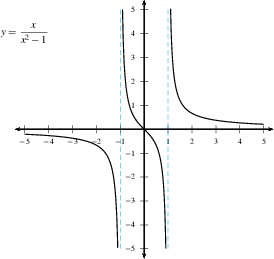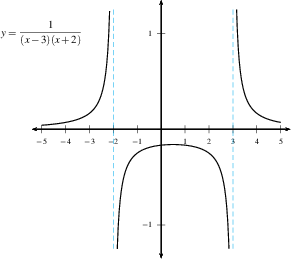
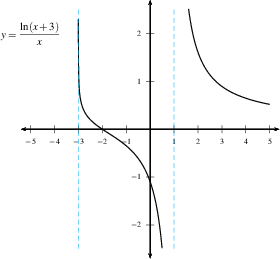
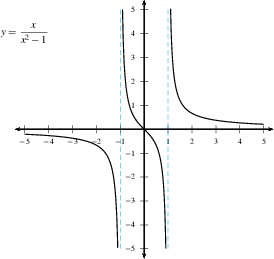
Warning:  when we say a limit $=\infty$, technically the limit doesn't exist.  $\displaystyle\lim_{x\to a}f(x)=L$ makes sense (technically) only if $L$ is a number.  $\infty$ is not a number!  (The word "infinity" literally means without end.)  If the limit is $+ \infty$, then the function increases without end. If the limit is $-\infty$, it decreases without end.  We say a limit is equal to $\pm\infty$ just to indicate this increase or decrease, which is more information than we would get if we simply said the limit doesn't exist.

Vertical Asymptotes

Definition: The line $x=a$ is a vertical asymptote of a function $f$ if the limit of $f$ as $x\to a$  from the left and/or right is $\pm\infty$.  This means at least one of the following is true:

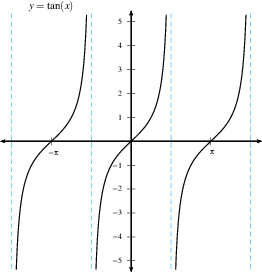
$$\lim_{x \rightarrow a^+}f(x) = \infty,$$ $$\lim_{x \rightarrow a^-}f(x) = \infty,$$ $$\lim_{x \rightarrow a^+}f(x) = -\infty,$$ $$\lim_{x \rightarrow a^-}f(x) = -\infty.$$

Here are some examples of graphs with one or more vertical asymptotes. 
DO:  Find all vertical asymptotes in the following graphs.