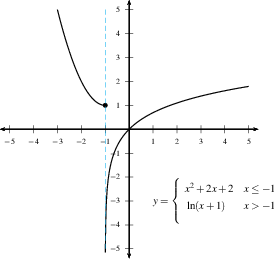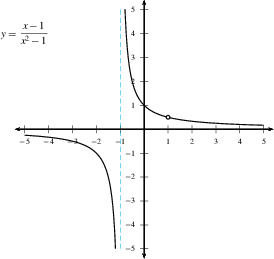- If $\displaystyle{\lim_{x \to a^+} f(x)}$ and
$\displaystyle{
\lim_{x \to a^-} f(x)}$ both exist, but are different,
then we have a jump discontinuity. (See the
example below, with $a=-1$.)

-
If either $\displaystyle{\lim_{x \to a^+} f(x)} = \pm
\infty$ or $\displaystyle{\lim_{x \to a^-} f(x)} = \pm
\infty$, then we have an infinite discontinuity,
also called an asymptotic discontinuity. (See
the example below, with $a=-1$.)
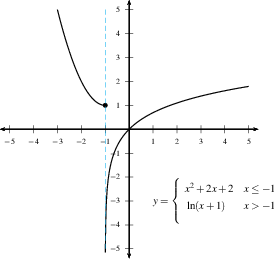
-
If $\displaystyle{\lim_{x \to a^+} f(x)}$ and
$\displaystyle{\lim_{x \to a^-} f(x)}$ exist and are
equal (and finite), but
$f(a)$ happens to be different (or doesn't exist), then
we have a removable discontinuity, since by
changing the value of $f(x)$ at a single point we can
make $f(x)$ continuous. (See the example below, with
$a=1$.)
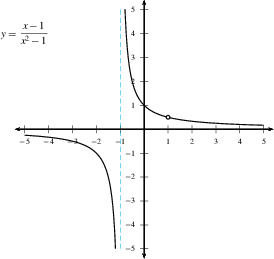
|