Determining Intervals of Concavity and Inflection Points

The intervals of concavity can be found in the same way used to determine the intervals of increase/decrease, except that we use the second derivative instead of the first. In particular, since $(f')'=f''$, the intervals of increase/decrease for the first derivative will determine the concavity of $f$.

The process to find intervals of concavity


  1. If possible, factor $f''$.  If $f''$ is a quotient, factor the numerator and denominator (separately).

  2. Find all critical numbers $x=s$ of $f'$.   These are the points where $(f')'=0$ or $(f')'$ doesn't exist (i.e., the points where $f''=0$ or where $f''$ doesn't exist).  You might want to call these $s$ subcritical numbers.

  3. Draw a number line with tick marks at each subcritical number $s$.

  4. For each interval between subcritical numbers in which the function $f$ is defined, pick a number $b$, and then find the sign of the second derivative $f''(b)$.

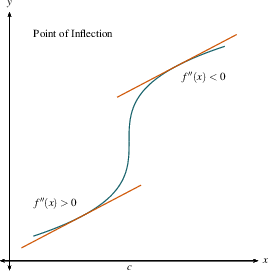
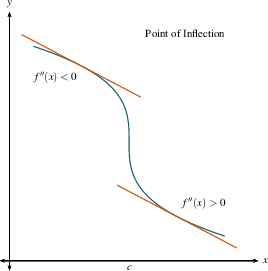
  5. If $f''(b) \gt 0$, then $f'$ is increasing on the interval containing $b$.  This means that the slopes are increasing, so $f$ is concave up.  Draw a right-side-up bowl over that interval on your number line.  Similarly, if $f''(b) \lt 0$, draw an upside-down bowl.

  6. That's it! You can now see the intervals where $f$ is concave up or down.

If this box above looks familiar, it is because we use that exact same process to find intervals of increase/decrease of $f$, by looking at $f'$ instead of $f''$.  Keep in mind:  the sign of $f'$ indicates the direction (up or down) of $f$, while the sign of $f''$ indicates the concavity of $f$.

Inflection points

An inflection point is a point where concavity changes.  In each of the graphs below, the point of inflection lies between the location of the two tangent lines; the tangent lines show that the concavity has changed. 
DO:  The inflection point is not marked -- can you find it?


                         


The process to find inflection points

Take the number line showing subcritical numbers and intervals of concavity from the process above.  The points $(s,f(s))$ where the concavity changes are inflection points.  Note:  not all subcritical numbers will yield inflection points (just like not all critical numbers yield local extrema).

Example: Find the intervals of concavity and any inflection points of f(x)=x3−3x2 .

DO:  Try to work this problem, using the process above, before reading the solution.

Solution: Since f′(x)=3x2−6x=3x(x−2), our two critical points for f are at x=0 and x=2.  We used these critical numbers to find intervals of increase/decrease as well as local extrema on previous slides.  Meanwhile, f″(x)=6x−6 , so the only subcritical number is at x=1.  It's easy to see that f″ is negative for x<1 and positive for x>1 , so our curve is concave down for x<1 and concave up for x>1 , and thus there is a point of inflection at x=1.