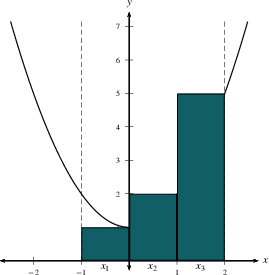
The main ideas of approximating areas with sums is developed further, in the following video. In it, we consider the area under the parabola $y=1+x^2$ between $x=-1$ and $x=2$. Some of the calculations are reproduced below the video.

We are trying to find the area under the curve $y=f(x)=1+x^2$ between $x=1$ and $x=2$. Since the whole is the sum of the parts, we break the region from $x=-1$ to $x=2$ into three pieces, one from $-1$ to 0, one from 0 to 1, and one from 1 to 2. We estimate the area of each piece, add up the areas, and get an estimate for the total area under the curve.

Our first attempt is using right endpoints. We use $f(0)$ to estimate the height of the first region, $f(1)$ to estimate the height of the second, and $f(2)$ to estimate the height of the third. Since each strip has width $(2-(-1))/3=1$, we take the area of each strip to be height $\times$ width = f(right endpoint) $\times$ 1. \begin{eqnarray*} \hbox{Area of first strip }& \approx & 1 f(0) = 1 \cr \hbox{Area of 2nd strip }& \approx & 1 f(1)=2 \cr \hbox{Area of first strip }& \approx & 1 f(2)=5 \cr \hbox{Total area }& \approx & 1+2+5 = 8. \end{eqnarray*}

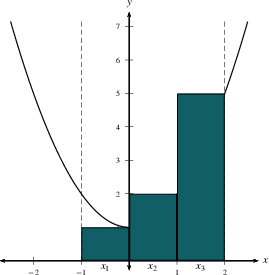
Our second attempt is using left endpoints. Here we use $f(-1)$ to estimate the height of the first region, $f(0)$ for the second, and $f(1)$ for the third. We then have: \begin{eqnarray*} \hbox{Area of first strip }& \approx & 1 f(-1) = 2 \cr \hbox{Area of 2nd strip }& \approx & 1 f(0)=1 \cr \hbox{Area of first strip }& \approx & 1 f(1)=2 \cr \hbox{Total area }& \approx & 2+1+2 = 5. \end{eqnarray*}

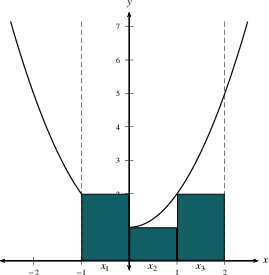
A third method, not covered in the video is to use midpoints. Here we use $f(-1/2)$ to estimate the height of the first region, $f(1/2)$ for the second, and $f(3/2)$ for the third. We then have: \begin{eqnarray*} \hbox{Area of first strip }& \approx & 1 f(-1/2) = 5/4 \cr \hbox{Area of 2nd strip }& \approx & 1 f(1/2)=5/4 \cr \hbox{Area of first strip }& \approx & 1 f(3/2)=13/4 \cr \hbox{Total area }& \approx& \frac54 + \frac54 + \frac{13}{4} = \frac{23}{4} =5.75. \end{eqnarray*}

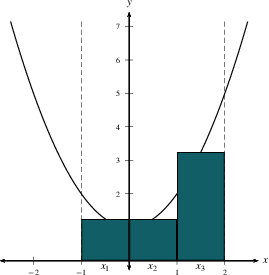
By the way, the actual area is 6. Of the three methods, the midpoint method came closest. But in truth, if we want to accurately estimate the area, we should break things into 30 strips, or 300, and not just 3. We'll soon learn how to take the limit of this sort of sum.