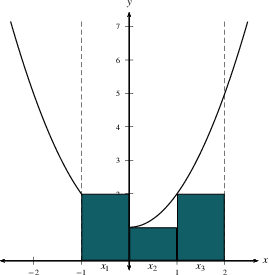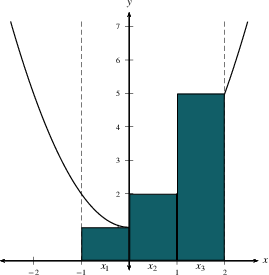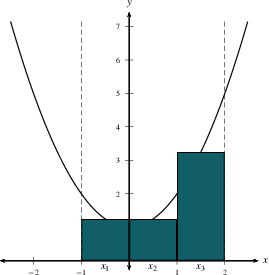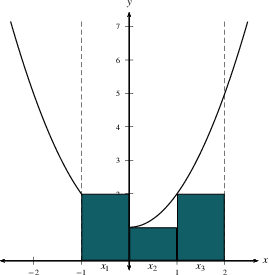
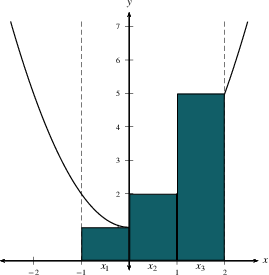
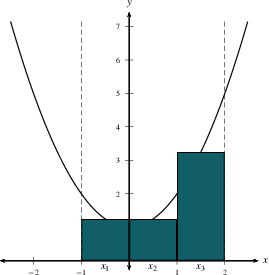
The total area under
$y=f(x)$ on an interval is approximated
by $$\sum_{i=1}^n \,f(x_i^*)\, \Delta x,$$ which is the sum of the
areas of $n$ rectangles. This sort of expression is called a
Riemann Sum. We use the
Greek letter sigma ($\Sigma$) to mean
sum. The expression
$\displaystyle{\sum_{i=1}^n (\hbox{formula involving $i$})}$ means
"plug $i=1$ into the formula, then plug in $i=2$, all the way up
to $i=n$, and add up the terms." Thus:
$$\sum_{i=1}^n \,f(x_i)\, \Delta x=\,f(x_1)\, \Delta x +\,f(x_2)\, \Delta x+\,f(x_3)\, \Delta x+\cdots+\,f(x_{n-1})\, \Delta x+ \,f(x_n)\, \Delta x.$$
In the video, keep referring to the left side for a list of
symbols. You will need to learn the meaning of, and how to find,
the values represented by $a,b,n,\Delta x,x_i$ and $f(x_i)$.
Notation:
|
The exact area is the limit of the Riemann sum as $n \to
\infty$. Notice that we could use the left
endpoint $x_{i-1}$, the right
endpoint $x_i$, the midpoint
$\frac{x_{i-1}+x_i}{2}$, or any other representative point.