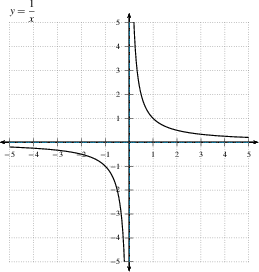- A limit as $x \to \infty$ (or $x \to -\infty$) describes what happens when $x$ increases (or decreases) without bound.
- The limit laws apply to limits as $x \to \pm \infty$, just as they apply to limits as $x \to a$ or $x \to a^+$ or $x \to a^-$.
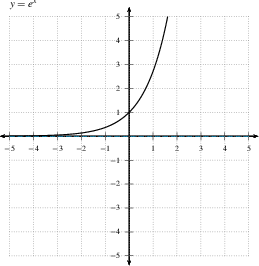
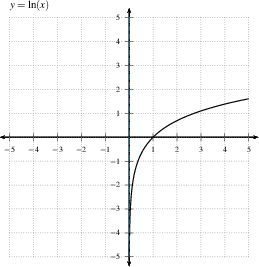
- An asymptote is a line that the graph $y=f(x)$ approaches. This line can be vertical, horizontal, or diagonal. A curve can be an asymptote too.
- A horizontal asymptote
is approached as $x \to \infty$ or as $x \to -\infty$. If
$\displaystyle{\lim_{x \to \infty} f(x) = L}$ or
$\displaystyle{\lim_{x \to -\infty} f(x) = L}$, then $y=L$ is a horizontal asymptote -- a
horizontal asymptote is a line, and must be given as the
equation of a line. A curve may
cross its horizontal asymptote.
- A vertical asymptote is
approached as $y \to \infty$ or as $y \to -\infty$, which only
happens if the function increases without bound at a finite
value. If $\displaystyle{\lim_{x \to a^+} f(x) = \pm \infty}$
or $\displaystyle{\lim_{x \to a^-} f(x) = \pm \infty}$, then
the function has a vertical asymptote at $x=a$ -- a vertical asymptote is a
line, and must be given as the equation of a line. A curve cannot cross a vertical asymptote --
it is not defined there.
DO: You should recognize all of
the asymptotes of the following graphs (if they have
any). You should know the functions for all but the
2nd and 3rd graphs without looking at the labels.