
(Animations from Barry McQuarrie)
To get the instantaneous velocity at a particular time $t=a$, we average over shorter and shorter time intervals. That is, we compute the average velocity between time $a$ and $a + \Delta t$, and then take a limit as $\Delta t \to 0$. On a graph, this is taking the slope of secant lines between points that are getting closer and closer. In the limit, we get the slope of a tangent line.
Whether we think in terms of velocity or slope, we get a limit: $$\lim_{\Delta t \to 0} \frac{s(a+\Delta t)-s(a)}{\Delta t}.$$ This can also be written as: $$\lim_{t \to a} \frac{s(t)-s(a)}{t-a},$$ where $t=a+\Delta t$. This quantity (if the limit exists) is called the derivative of $s(t)$ at time $t=a$.
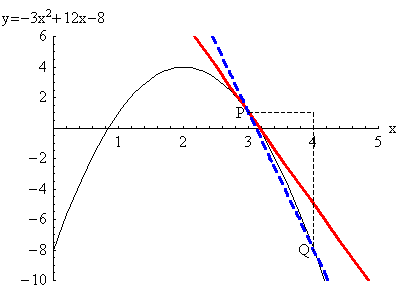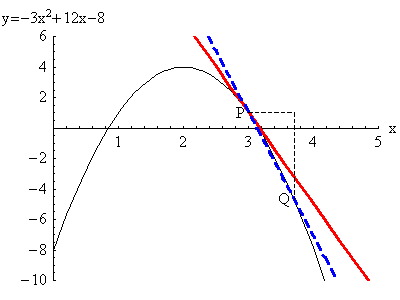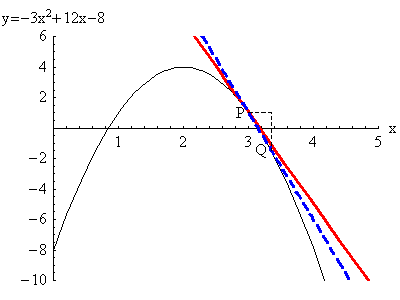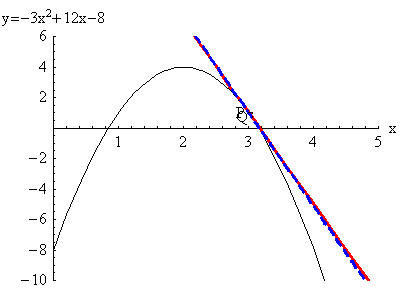
In the animations below, \(a=3\), the \(x\) coordinate of point
\(P\); and \(a+\Delta x\) is the \(x\)-coordinate of point
\(Q\). The movement is the point $Q$ approaching the point
$P$, which means $3+\Delta x$ is getting closer to $3$, which
means $\Delta x$ is getting closer to $0$.
The red tangent line (at $P$) is the limit of the blue secant
lines through $P$ and $Q$. Note that $\Delta x$ can be positive
(first animation) or negative (second animation). For the
derivative to exist, the limits as $\Delta x \to 0^+$ and $\Delta
x \to 0^-$ must give the same answer.


(Animations from Barry McQuarrie)