Concavity and the relationship between $f,f'$ and $f''$
Concavity
Definitions:
- If the graph of $f$ lies above all of its tangent
lines on an open interval, the we say it is concave
up on that interval.
- If the graph of $f$ lies below all of its tangent
lines on an open interval, then we say it is concave
down on that interval.
- A point, $P$, on a continuous curve $f(x)$ is an inflection
point if $f$ changes concavity there.
|
When a curve is concave up, it is sort
of bowl-shaped, and you can think it might hold water, with the rim
pointing up. Notice that a function that is concave up may be increasing or
decreasing:
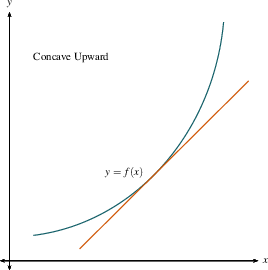

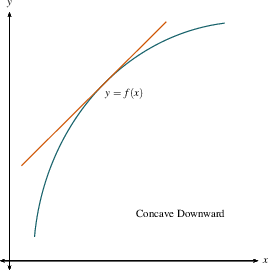
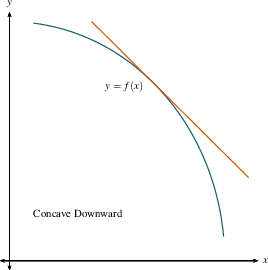
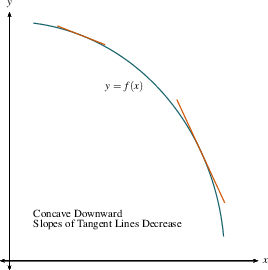
Similarly, when a curve is concave down,
it is sort of upside-down-bowl-like, and water would run off of it,
with the rim pointing down. Notice
that a function that is concave down may be
increasing or decreasing:
$f$, $f'$ and $f''$
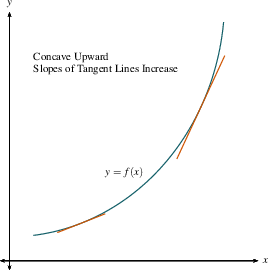
When the slopes of tangent lines are increasing, i.e. when $f'$
is increasing, the function is concave up, as you can see below in
the first two graphs. Since $(f')'=f''$, when $f'$ is
increasing, $f''$ is positive. Similarly, when the slopes of
tangent lines are decreasing, i.e. when $f'$ is decreasing, the
function is concave down, as you can see in the second two graphs
below. Since $(f')'=f''$, when $f'$ is decreasing, $f''$ is
negative.
DO: Spend some time
looking at the slopes and concavity below, and work to totally
understand the relationships between $f,f'$ and $f''$ indicated
below the graphs.

$$
\Large{f''>0\quad\Longleftrightarrow\quad f'\uparrow\quad
\Longleftrightarrow\quad f \cup}$$

$$\Large{
f''<0\quad\Longleftrightarrow\quad f'\downarrow\quad
\Longleftrightarrow\quad f \cap}$$









