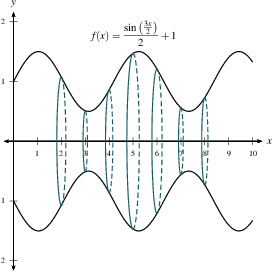
The hard part about getting volumes from integration is figuring out the cross-sectional area $A(x)$. In general, this requires some knowledge of geometry. But if we have a solid of revolution, the geometry is easy:

| $$\int_a^b A(x)\, dx = \pi \int_a^b f(x)^2\, dx.$$ |