Examples of Infinite Sequences

Consider the sequence $\{a_n\}=\{a_n\}_{n=1}^\infty=a_1,a_2,a_3,\ldots$.  Recall that this sequence is graphed by letting the horizontal axis be the $n$-axis, and $a_n$ the height of the dot.  We look at the graphs of a number of examples of (infinite) sequences below.  We can get a visual idea of what we mean by saying a sequence converges or diverges.  These examples are discussed in the video that follows.

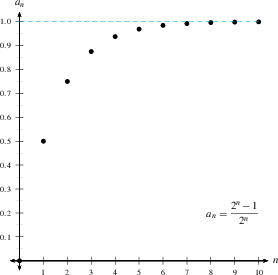
1)  $\displaystyle\frac12, \, \frac34,\, \frac78,\, \frac{15}{16}, \, \frac{31}{32},\ldots$ converges to 1.
2)  The digits of $\pi$, namely 3, 1, 4, 1, 5, 9, $\ldots$, diverge.
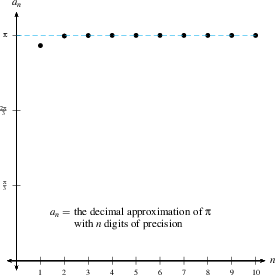
3)  The decimal approximations of $\pi$, namely 3, 3.1, 3.14, 3.141, $\ldots$, converge to $\pi$.
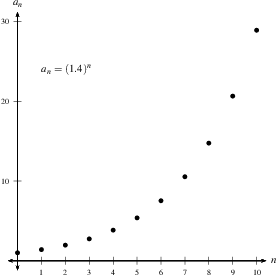
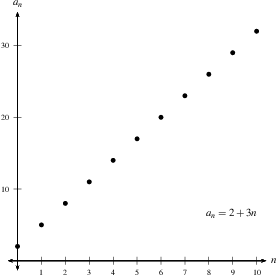
4)  Arithmetic sequences, which are sequences where the difference between successive terms is constant ($(a_{n+1}-a_n)$ is constant), such as 2, 5, 8, 11, 14, $\ldots$, always diverge (unless the terms are all the same).
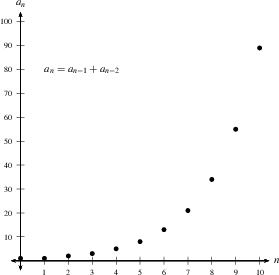
5)  The Fibonacci sequence 1, 1, 2, 3, 5, 8, $\ldots$ diverges.
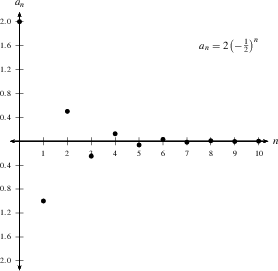
6)  The sequence $\displaystyle 2, \, -1,\, \frac12,\, -\frac14,\,\frac18,\, -\frac{1}{16}, \ldots$ is an example of a geometric sequence (see below; here, $a=2$ and $r=-\tfrac 1 2$).  This sequence converges to 0.
7)  Geometric sequences  are sequences where the ratio of successive terms is constant. They look like$$\{ar^n\}_n= a,\,ar,\,ar^2,\,ar^3\ldots$$with the constant ratio $r$.  A geometric sequence converges if $-1<r\le1$ and diverges otherwise.  (We can see that if $r=1$, this sequence is the constant sequence, $a,a,a,\ldots$, which converges to $a$.)