Examples 5-7

In the previous Examples 3 and 4, the way we specified $D$ and $R$ suggested how to write the integral as a iterated integral.  Sometimes conditions are best interpreted graphically before deciding on whether to evaluate as Type I or Type II.

Example 5:  Evaluate the integral $\displaystyle I \ = \iint_D\, (3x +4y)\, dA$,
where $D$ is the bounded region enclosed by $y = x$ and $y=x^2$.

DO:  Without looking, graph the region $D$.  Set up a Type I integral.


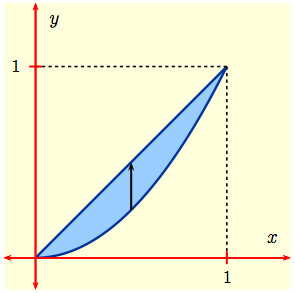
Solution 5:  $D$ is enclosed by the straight line $y = x$ and the parabola $y = x^2$ as shown here. To determine the limits of integration we first need to find the points of intersection of $y = x$ and $y = x^2$. These occur when $x^2 = x$.  This means $x(x-1)=0$, so $x = 0,\, 1$.
Treating $D$ as a Type I region, we fix $x$ between $x=0$ and $x=1$, and integrate with respect to $y$ along the black vertical line, getting the iterated integral $\displaystyle I \ = \ \int_0^1\left(\int_{x^2}^{x}\, (3x + 4y)\, dy\right)\,dx$ 
DO:  Evaluate $I$.

------------------------------------------------------------------------------

In Example 5 it was simpler to fix $x$ and integrate first with respect to $y$ because the bounding curves were already given to us in terms of $x$, as $$y \ = \ f_1(x)\ = \ x^2\,,\qquad y \ = \ f_2(x)\ = \ x\,.$$ Had they been given as $x \,=\, g_1(y)$ and $x\,=\, g_2(y)\,$ it might have been easier to think of $D$ as a Type II region. We would fix $y$ and first integrate with respect to $x$.  Sometimes the geometry of the region of integration makes it obvious whether we have Type I or Type II, as in the following examples (which we will not evaluate).

Example 6:  The region $D$ that is shown here is Type I but is not Type II:  Fixing $x$ and integrating first with respect to $y$ along the vertical black line makes good sense because then we have the same curve $f_1(x)$ along the bottom and $f_2(x)$ along the top: $$ D \ = \ \Bigl\{\,(x,\,y) : f_1(x) \le y \le f_2(x),\ \ a \le x \le b\,\Bigl\}$$ for suitable choices of $a,\, b$ and functions $f_1(x),\, f_2(x)$ giving us: $$ \iint_D\, f(x,\,y)\, dA = \int_a^b \left(\int_{f_1(x)}^{f_2(x)}\, f(x,\,y)\, dy\right) dx\,.$$But if we had chosen to fix $y$, then the integral with respect to $x$ would sometimes split into two parts, as is shown with the red horizontal lines.  This would make evaluate of this integral more complicated -- for one thing, there would be more than one integral.



------------------------------------------------------------------------------


Example 7:  Similarly, the region $D$ shown here is Type II but not Type I.  Fixing $y$ and integrating first with respect to $x$ along the horizontal black line makes good sense because then $$ D \ = \ \Bigl\{\,(x,\,y) : g_1(y) \le x \le g_2(y),\ \ c \le y \le d\,\Bigl\}$$ for suitable choices of $c,\, d$ and functions $g_1(y),\, g_2(y)$.  In this case $$ \iint_D\, f(x,\,y)\, dxdy = \int_c^d \left(\int_{g_1(y)}^{g_2(y)}\, f(x,\,y)\, dx\right) dy\,.$$But if we had chosen to fix $x$, then the integral with respect to $y$ would sometimes splits into two parts as shown by the red vertical lines.  Again, this would make the integral(s) more complicated.