The limit of a function is the limit of continuous values of the
function, while the limit of a sequence is a limit of discrete
numbers. Nonetheless, we recognize that if a continuous
function passes through all numbers of a sequence, then the
convergence or divergence of the sequence matches the convergence
or divergence of the function. To see this, just picture the
graph of a sequence (earlier in this module) and draw the curve
through the dots, letting the curve be $f(x)$, and hence
$f(n)=a_n$ for the positive integers $n$.
| Theorem
1: Let $f$ be a function with $f(n)=a_n$ for
all integers $n>0$. If $\displaystyle\lim_{x\to\infty}f(x)=L$, then $\displaystyle\lim_{n\to\infty}a_n=L$ also. |
Example 1: By the theorem, since $\displaystyle\lim_{x\to\infty}\frac{1}{x^r}=0$ when $r>0$, $\displaystyle\lim_{n\to\infty}\frac{1}{n^r}=0$ when $r>0$. Learn this example.
-------------------------------------------------------------------
Example 2: Evaluate $\displaystyle\lim_{n\to\infty}\frac{2n}{3n-4}$.
Solution 2: By dividing the top and the bottom by $n$, we get $\displaystyle\lim_{n\to\infty}\frac{2}{3-\tfrac 4 n}$. By the previous example, $\tfrac 4 n$ converges to 0, so we get $\displaystyle\lim_{n\to\infty}\frac{2n}{3n-4}=\frac{2}{3}$.
-------------------------------------------------------------------
Example 3: Evaluate $\displaystyle\lim_{n\to\infty}\frac{5n}{e^n}$. DO: To solve this limit, first compute $\displaystyle\lim_{x\to\infty}\frac{5x}{e^x}$ before reading on.
Solution 3: We use l'Hospital's Rule. $\displaystyle\lim_{x\to\infty}\frac{5x}{e^x}\underset{\fbox{$\tfrac \infty \infty\,,\, \text{l'H}$}}{=}\lim_{x\to\infty}\frac{5}{e^x}=0$. Thus $\displaystyle\lim_{n\to\infty}\frac{5n}{e^n}=0$ by Theorem 1.
Notice that we cannot take a derivative of a sequence, since a derivative exists only if the function is continuous, and sequences are not continuous. Yet, because of our theorem, we can use l'Hopital's rule on the associated (continuous) $f(x)$ and compute our limit by taking derivatives. We get the limit of the sequence by evaluating the limit of the function.
| Theorem 2: $\displaystyle
\lim_{n\to\infty}a_n=0$ if and only if
$\displaystyle\lim_{n\to\infty}|a_n|=0$. Warning: This is only true when the limits are equal to 0. |
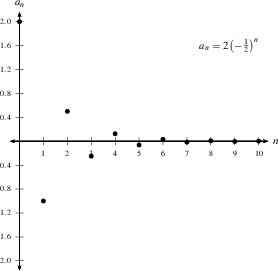
To see why this theorem makes sense, think about this graph of a sequence $a_n=2\frac{(-1)^n}{2}$, which converges to 0. The graph of $\left\{|a_n|\right\}$ would flip all the negative points to their positive values, giving a sequence steadily decreasing to zero. |
|
-------------------------------------------------------------------Example 4: By Theorem 1, since $\displaystyle\lim_{x\to\infty}r^x=0$ when $0<r<1$ (remember exponential functions?), $\displaystyle\lim_{n\to\infty}r^n=0$ when $0<r<1$. By Theorem 2, this extends to $-1<r<1$. If $r>1$ or $r\le-1$, the limit diverges. (DO: what happens when $r=1$?) Summarizing:
$\displaystyle\lim_{n\to\infty}r^n \left\{\begin{array}{ll}\text{converges }&\text{ if }-1<r\le 1\\\text{diverges}&\text{otherwise}\end{array}\right.$ Learn this. We will use it frequently.
Example 5: Let $ a_n=(-1)^n\frac{3^{n+2}}{5^n}$. We will take the the absolute value of our sequence, which here simply means ignoring the alternating sign $(-1)^n$, and take a limit to see if we get 0. Rewrite to get $|a_n|=3^2\left(\frac{3}{5}\right)^n=9\left(\frac{3}{5}\right)^n$. We evaluate
$\displaystyle\lim_{n\to\infty}|a_n|= \lim_{n\to\infty}\frac{3^{n+2}}{5^n}=9\left(\frac{3}{5}\right)^n=9\cdot 0=0$, by Example 4 with $r=\tfrac 3 5$, since $-1<r<1$. Therefore,
$\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}(-1)^n\frac{3^{n+2}}{5^n}=0$ by Theorem 2.
