The Integral Test

Integral Test:  If $f$ is a continuous, positive and decreasing function where $f(n)=a_n$ on the interval $[1,\infty)$, then
the improper integral $\displaystyle\int_1^\infty f(x)\, dx$ and the infinite series $\displaystyle\sum_{n=1}^\infty a_n$
either both converge or both diverge.

Picture infinitely many rectangles of width 1 and height $a_n$, so the area of the $n^{th}$ rectangle is $a_n$.  Then the series $\displaystyle\sum_{n=1}^\infty a_n$ is equal to the sum of the areas of these infinitely many rectangles.  See the graphic examples below.


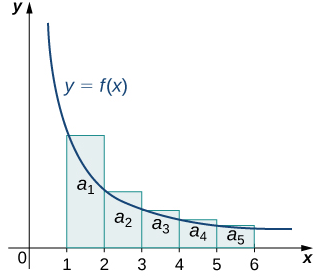
Consider this graph.  We see that the value of the series from $a_2$ on is less than the area under the curve $f$ from 1 to infinity; i.e.
$\displaystyle\sum_{n=2}^\infty a_n<\int_1^\infty f(x)\,dx$.  If this integral converges to some finite value $C$, then by using this inequality and doing a little work, we get $\displaystyle\sum_{n=1}^\infty a_n= a_1+\sum_{n=2}^\infty a_n<a_1+\int_1^\infty f(x)\,dx=a_1+C<\infty$, so the series is finite, and thus the series converges. 


archive.cnx.org

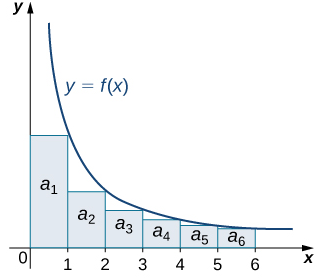
Now consider this graph.  We see that the sum of the same series beginning with $a_1$ is larger than the area under the same curve $f$ from 1 to infinity; i.e.
$\displaystyle\int_1^\infty f(x)\,dx<\sum_{n=1}^\infty a_n$.   If this integral diverges, then because of our constraints on $f$ it diverges to infinity.  Since the area under $f$ is infinite, then the sum of the areas of the rectangles must also be infinite, i.e. $\displaystyle\sum_{n=1}^\infty a_n$ is infinite, and thus the series diverges.  We see that if the integral diverges, so does the series.

archive.cnx.org
Summary:  either both the integral and the series converge, or both diverge.


From our work with improper integrals, you may have seen that the improper integral
$\displaystyle\int_1^\infty\frac{1}{x^p}\,dx$ converges if $p>1$, and diverges if $p\le 1$.
By using the integral test, we therefore get our $p$-series test, which is extremely useful, especially when used to find comparable series for the comparison tests. 

$\displaystyle{\sum_{n=1}^\infty \frac{1}{n^p}}$ converges if $p>1$ and diverges if $p \le 1$.

Explanation and examples of the integral test, as well as determining the above integral of $\frac{1}{x^p}$ and the $p$-series test are included on the first video.  The second video includes detail of the graphical information above.