Examples of Iterated Integrals
Example 1: (from the video) Compute
$\displaystyle\iint_R(x-y)^2\,dA$ over the region with $x$ in
$[0,2]$ and $y$ in $[0,1]$. As we will soon see, by Fubini's
Theorem, $dA=dx\,dy$ or $dA=dy\,dx$; i.e. we can fix $x$ and
integrate with respect to $y$ first, or vice versa.
Solution 1: We will compute
$\displaystyle\iint_R(x-y)^2\,dA=\int_0^2\int_0^1
(x-y)^2\,dy\,dx=\int_0^2\left(\int_0^1 (x-y)^2\,dy\right)\,dx$.
DO: Integrate the parenthetical
integral $\displaystyle\int_0^1 (x-y)^2\,dy$, treating $x$ as a
constant, before reading more.
First we compute the antiderivative, then evaluate it (if you can do
this substitution in your head, you can just evaluate the
integral). Remember, $y$ is our
variable and $x$ is a constant.
$\displaystyle\int (x-y)^2\,dy\overset{\fbox{$ \,\,u\,=\,x-y\\
du\,=\,(-1)\,dy$}\\}{=} -\int u^2\,du=-\frac{1}{3}u^3+c $, so
$\displaystyle\int_0^1 (x-y)^2\,dy=-\frac{1}{3}(x-y)^3
\left|\begin{array}{c} ^1 \\ _0\end{array}\right
.=-\frac{1}{3}\left((x-1)^3-(x-0)^3\right)=\frac{x^3-(x-1)^3}{3}$
DO: Integrate the outside
integral, with the integrand being our answer from above:
$\displaystyle\int_0^2\frac{x^3-(x-1)^3}{3}\,dx$ before reading
more.
Here, we can see our antiderivative (after a mental substitution
$u=x-1$, where $du=dx$)
$\displaystyle\int_0^2\frac{x^3-(x-1)^3}{3}\,dx=\frac{1}{3}\left(\frac{x^4}{4}-\frac{(x-1)^4}{4}\right)\left|\begin{array}{c}
^2 \\ _0 \end{array}\right
.=\frac{1}{3}\left(\left(4-\frac{1}{4}\right)-\left(0-\frac{1}{4}\right)\right)=\frac{4}{3}$
In these two steps, one variable at a time, we have found
$\displaystyle\iint_R(x-y)^2\,dA=\int_0^2\left(\int_0^1
(x-y)^2\,dy\right)\,dx=\int_0^2\left(\frac{x^3-(x-1)^3}{3}\right)\,dx=\frac{4}{3}$
----------------------------------------------------------------------------
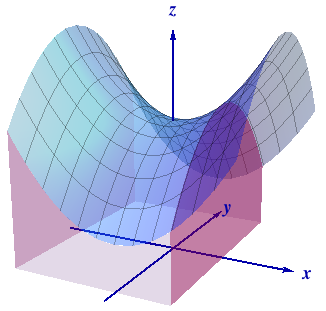
Example 2: Find the volume of the solid $W$ under the
hyperbolic paraboloid $$z=f(x,
y) = 2+ x^2 - y^2 $$ and over the square $D\,=
\,[-1,\,1]\,\times\,[-1,\,1]$.
DO: Compute this integral before
reading more. This is the graph of $f$:
Solution 2: We will compute
$\displaystyle\int_{-1}^1\int_{-1}^1\, (2+x^2 - y^2)\, dy\,dx$.
$\displaystyle\int_{-1}^1\left(\int_{-1}^1\, (2+x^2 - y^2)\,
dy\right)\,dx=\int_{-1}^1\left[\,2y +x^2y
-\frac{y^3}{3}\right]_{-1}^1\,dx$ (after integration with respect to
$y$, leaving $x$ constant)
$\displaystyle=\int_{-1}^1\left[(2+x^2-1/3)-(-2-x^2+1/3)\right]\,dx
=\int_{-1}^1\left(\frac{10}{3} +2x^2\right)\,dx$ (and now integrate
with respect to $x$)
$\displaystyle=\left(\frac{10}{3}x+\frac{2}{3}x^3\right)\left|\begin{array}{c}
^1 \\ _{-1} \end{array}\right
.=\frac{10}{3}+\frac{2}{3}-\left(-\frac{10}{3}-\frac{2}{3}\right)=8$