Examples 1-4

In the following video, we will compute Example 1 and Example 2:


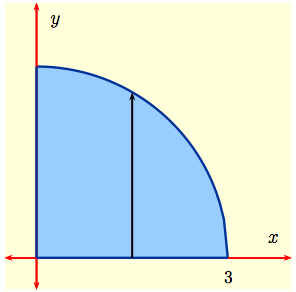
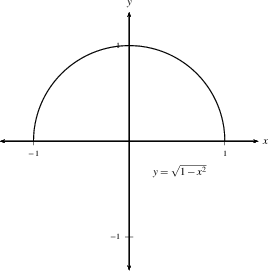
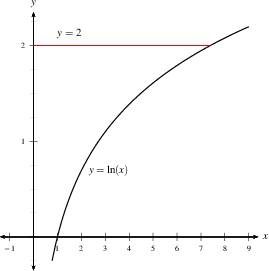Example 1:  Evaluate $$\iint_R f(x,y)\,dA,$$ where $f(x,y)= x^2y$ and $R$ is the upper half of the unit disk (shown here).

Example 2:  Evaluate $$\iint_R f(x,y)\,dA,$$ where $f(x,y) = 4xe^{2y}$ and the region $R$ is bounded by the $x$-axis, the $y$-axis, the line $y=2$ and the curve $y=\ln(x)$ (shown here).




Now, we look at some additional examples.

Example 3: Evaluate the integral $$I \iint _D\, (x+y)\, dA$$ where $D$ consists of all points $(x,\,y)$ such that $0 \ \le \ y \ \le \sqrt{9-x^2}\,, \quad 0\ \le \ x \ \le 3\,.$

DO:  Graph the region $D$ before reading further.  Then try to set up a Type I iterated integral.
Solution 3:  Since $y^2 \ = \ 9 - x^2$ is a circle of radius $3$ centered at the origin, $D$ consists of all points in the first quadrant inside this circle as shown here.  This is described as a Type I region, so we
  • fix $x$ in and integrate with respect to $y$ along the black vertical line as shown, and
  • then integrate with respect to $x$ from $x=0$ to $x=3$ (all possible black vertical lines).
So the double integral $I$ becomes the interated integral
\begin{eqnarray}
\int_0^3\left(\int_0^{\sqrt{9-x^2}}\, (x+y)\, dy\right)\,dx
&=& \int_0^3\, \Bigl[\, xy +\frac{1}{2}y^2 \,\Bigl]_0^{\sqrt{9 - x^2}}\,dx\\
&=&\int_0^3\, \Bigl( x\sqrt{9 - x^2} +\frac{1}{2} (9 - x^2)\Bigr)\, dx\\
\end{eqnarray}

DO:  Evaluate the above integral.  The answer is 18.

----------------------------------------------------------------------------------

Example 4:  Evaluate the integral $\displaystyle I=\iint_R\, (x+y)\, dA,$ where $R$ consists of all points $(x,y)$ with $0\le y\le 3$ and $0\le x\le\sqrt{9-y^2}$.

DO:  Graph this region $R$.  Is it the same as $D$ above?  Set up and evaluate the integral above as a Type II integral over $R$, which will have black horizontal lines.  You should get the same answer as in Example 3.