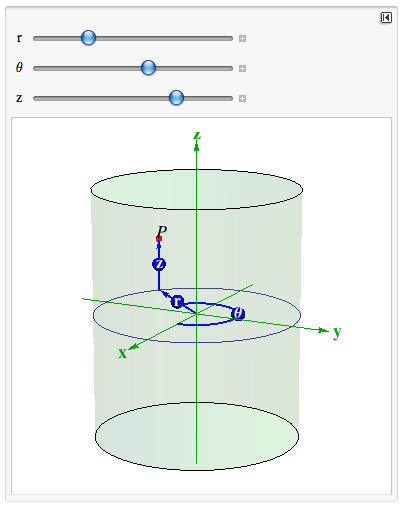
Cylindrical Coordinates: When there's symmetry about an axis, it's convenient to take the $z$-axis as the axis of symmetry and use polar coordinates $(r,\, \theta)$ in the $xy$-plane to measure rotation around the $z$-axis. Check the interactive figure to the right. A point $P$ is specified by coordinates $(r,\, \theta, \, z)$ where $z$ is the height of $P$ above the $xy$-plane.
(i) What happens to $P$ as $z$ changes?
(ii) What's the relation between $r$, $P$ and the axis of symmetry?
(iii) What are the natural restrictions on $\theta$?
(iv) The relation between Cartesian coordinates $(x,\,y,\,z)$ and Cylindrical coordinates $(r,\, \theta, \, z)$ for each point $P$ in $3$-space is $$ x \ = \ r \cos \theta,\qquad y \ = \ r \sin \theta, \qquad z \ = \ z\,.$$