Now that we know what double integrals are, we can start to compute them. The key idea is: One variable at a time!
In order to integrate over a rectangle $[a,b] \times [c,d]$, we first integrate over one variable (say, $y$) for each fixed value of $x$. That's an ordinary integral, which we can do using the fundamental theorem of calculus. We then integrate the result over the other variable (in this case $x$), which we can also do using the fundamental theorem of calculus. So a 2-dimensional double integral boils down to two ordinary 1-dimensional integrals, one inside the other. We call this an iterated integral.
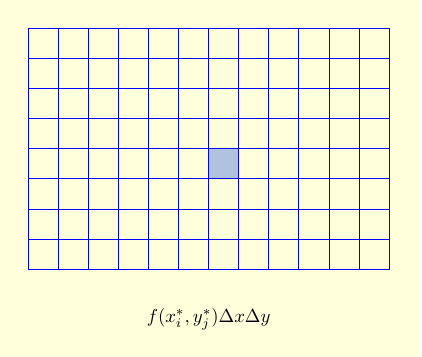
There are two ways to see the relation between double integrals and iterated integrals. In the bottom-up approach, we evaluate the sum $$\sum_{i=1}^m \sum_{j=1}^n f(x_{i}^*,y_{j}^*) \Delta x \Delta y,$$ by first summing over all of the boxes with a fixed $i$ to get the contribution of a column, and then adding up the columns. (Or we can sum over all of the boxes with a fixed $j$ to get the contribution of a row, and then add up the rows.)
| $f(x_{i}^*,y_{j}^*) \Delta y \Delta x$ is the approximate contribution of a single box to our double integral. |
|
| $\sum_{j=1}^n f(x_{i}^*,y_{j}^*) \Delta y \Delta x$ is the approximate contribution of all the boxes in a single column. As $n \to \infty$, the sum over $n$ turns into an integral, and we get $\left (\int_c^d f(x_i^*, y)dy \right ) \Delta x$. |
|
| Adding up the columns then gives $\sum_{i=1}^m \left (\int_c^d f(x_i^*, y) dy \right ) \Delta x$. Taking a limit as $m \to \infty$ turns the sum into an iterated integral: $$\int_a^b \left ( \int_c^d f(x,y) dy \right ) dx.$$ |
|
This bottom-up approach is explained in the following video. (However, there is a small error. At the beginning it says that we're going to integrate over the rectangle $[0,1] \times [0,2]$, but for the rest of the video the region $R$ is actually the rectangle $[0,2] \times [0,1]$.)
An alternate approach to finding volumes (and hence double integrals)
- the so-called Slice Method - was formulated by
Cavalieri
and is expressed mathematically in
|
Cavalieri's Principle: let $W$ be a solid and $P_x,\, a \le x \le b,$ be a family of parallel planes such that
|
|
Example:
Find the volume of the solid $W$ under the
hyperbolic paraboloid
$$z \ = \ f(x,\, y) \ = \ 2+ x^2 - y^2 $$
and over the square $D\,= \,[-1,\,1]\,\times\,[-1,\,1]$.
Solution: The solid is shown to the right. When $P_x$ is the vertical slice perpendicular to the $x$-axis for fixed $x$ shown in purple, then $$A(x) =\int_{-1}^2\, (2+x^2 - y^2)\, dy\qquad \qquad$$ $$\qquad = \left[\,2y +x^2y -\frac{y^3}{3}\right]_{-1}^1= \frac{10}{3} +2x^2 \,.$$ But then by using the slider to fill out the solid, Cavalieri's Principle shows that $W$ has |
|
In other words, the volume of a region is the $\int_a^b A(x) dx$, where $A(x)$ is the cross-sectional area at a particular value of $x$. But that's the area under the curve $z=f(x,y)$, where we are treating $x$ as a constant and $y$ as our variable. That is, the double integral $\iint_R f(x,y)\, dA$ equals the iterated integral $\int_a^b \left (\int_c^d f(x,y) dy\right ) dx$.