History of Negative Numbers

Abbreviations:

• B.C.E. = Before Common Era (also known as B.C.)
• C.E. = Common Era (also known as A.D.)
• The notation [X,n] refers to page n of reference X.

c. 570 - 500 B.C.E., Greece: The Pythagoreans thought of number as "a multitude of units". Thus one was not a number for them. There are no indications of negative numbers in their work. [K, 50], [S, 257]

Fourth Century B.C.E., Greece: Aristotle made the distinction between number (i.e., natural numbers) and magnitude ("that which is divisible into divisibles that are infinitely divisible"), but gave no indications of the concept of negative number or magnitude. [K, 56], [S, 257]

c. 300 B.C.E., Greece: Books VII, VIII, and IX of Euclid's Elements concern the elementary theory of numbers. Euclid continues Aristotle's distinction between number and magnitude, but there are still no indications of negative numbers. [K, 84], [S, 257]

 c. 100 B.C.E.-50 C.E., China: In The Nine Chapters on the Mathematical Art (Jiuzhang Suanshu), negative numbers were used in the chapter on solving systems of simultaneous equations. Red rods were used to denote positive coefficients, black to denote negative ones. Rules for signed numbers were given. [K, 19] (For more information on the history of mathematics in China, see Mathematics in China, http://aleph0.clarku.edu/~djoyce/mathhist/china.html)

Third century C.E., Greece: The first indication of negative numbers in a western work was in Diophantus' Arithmetica, in which he referred to the equation which in modern notation would be represented as 4x + 20 = 0 as absurd, since it would give the solution x = -4. . He also said, "a number to be subtracted, multiplied by a number to be subtracted, gives a number to be added." So, for example, he could deal with expressions such as 9in modern notation) x - 1 times x - 2. However, Diophantus gave indications that he had no conception of the abstract notion of negative number [S, 258] [C, 61]

Seventh Century C.E., India: Negative numbers were used to represent debts when positive numbers represented assets. Indian mathematician/astronomer Brahmagupta used negative numbers to unify Diophantus' treatment of quadratic equations from three cases (ax² + bx = c, bx + c = ax², and ax² + c = bx) to the single case we are familiar with today. [C, 94]. He gave rules for operations with negative numbers. [K, 226]

Ninth Century C.E, Middle East.: Although the Arabs were familiar with negative numbers from the work of Indian mathematicians, they rejected them. [Kl, 192]Muhammad ibn Musa al-Khwarizmi's textbook Al-jabr wa'l- muqabala (from which we get the word "algebra") did not use negative numbers or negative coefficients [P]. Thus his discussion of quadratic equations dealt with six different types of equations, rather than the one general form we use. [K, 245]

Twelfth Century, India: Bhaskara gives negative roots for quadratic equations, but says the negative value "is in this case not to be taken, for it is inadequate; people do not approve of negative roots." [C. 93]

Thirteenth Century, China: Negative numbers were indicated by drawing a diagonal stroke through the right-most nonzero digit of a negative number. [S, 259]

Thirteenth Century, Italy:  Smith [S, 258] asserts that Fibonacci included no mention of negative numbers in his book Liber Abaci, but in a later volume, Flos, interpreted a negative solution in a problem as a loss. However, Mark Dominus (private communication) has pointed out that in Sigler's English translation of Liber Abaci there are some problems that do involve negative solutions, which are interpreted as debits. [Si, 226-227,320-322 , 484-486]

Fifteenth Century, Europe: Chuquet was the first to use negative numbers in a European work. He used them as exponents, writing, for example, 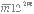for what we would write as -12x^-2. [K, 350]. However, he referred to them as "absurd numbers." [Kl, 252]

Sixteenth Century, Europe:

• Harriot did not accept negative roots, but sometimes placed a negative number along on one side of an equation. [Kl, 252]
• Cardan (Cardano), in his Ars Magna included negative solutions of equations and stated the basic laws of operating with negative numbers. [S, 259]. He called positive numbers numeri ueri (real) and negative numbers numeri ficti (fictitious). His used m: as a negative sign (for example, m:2 for -2). [S, 260] However, he did not allow negative coefficients in quadratic equations, since he interpreted these as partitioning squares in to rectangles of smaller size, and negative coefficients would mean these rectangles would need to have sides of negative length, an absurdity. Similarly, the negative solutions could not be interpreted within the geometric context. [P] (Compare with Brahmagupta's Seventh Century study of quadratic equations.) Cardano seemed to struggle with understanding negative numbers; for more details see Karen Parshall, The Art Of Algebra From Al-Khwarizmi To Viète: A Study In The Natural Selection Of Ideas, at http://www.lib.virginia.edu/science/parshall/algebra.html
• Bombelli similarly used m. to denote a negative number, and also used p. to denote a positive number (for example, p.3 for +3). [S, 260]
• Stevin used both positive and negative coefficients in equations, and accepted negative roots. [Kl, 253]
• Stifel refers to negative numbers as "absurd" or "fictitious below zero" [C, 141]. He did not accept them as roots of equations. However, he did accept them as coefficients, which enabled him to combine what had previously been considered three different types of equations into the single form x² = bx + c, where b and c were either both positive or had opposite signs. He also used negative numbers as exponents [K, 353].
• Tycho Brahe, the astronomer, referred to negative numbers as "privative," and used the minus sign.
• Viete did not acknowledge negative numbers.

Seventeenth Century, Europe:

• Hudde used letters with no sign prefix to denote either a positive or a negative number. [S, 259]
• Descartes partially accepted negative numbers. He rejected negative roots of equations as "false", since they represented numbers less than nothing. However, he showed that an equation with negative roots could be transformed into one having positive roots, which led him to accept negative numbers. [Kl, 252]
• "Pascal regarded the subtraction of 4 from 0 as utter nonsense." [Kl, 252]
• Wallis accepted negative numbers, but argued that they were "larger than infinity but not less than zero."
• The theologian and mathematician Antoine Arnauld argued against negative numbers by using proportions; to say that the ratio of -1 to 1 is the same as the ratio of 1 to -1 is absurd, since, "How could a smaller be to a greater as a greater is to a smaller?" [Kl, 252]

Eighteenth Century, Europe:

• Leibniz regarded Arnaud's objection to negative numbers as valid, but said the since the form of such proportions is correct, one could still calculate with them. [Kl, 252]
• Maclaurin treated negative quantities on a par with positive quantities in his A Treatise of Algebra in Three Parts. He refers to positive quantities as increment, negative as decrement. As examples, he gives excess and deficit; money due and money owed; lines to the right and to the left; and elevation above a horizon and depression below it. [K, 611]
• Euler started his Vollstandige Anleitung zur Algebra (Complete Introduction to Algebra) with a discussion of operations on positive and negative quantities. He uses the example of a debt to justify that a negative times a positive is a negative [K, 614]
• Maseres and Frend wrote algebra texts renouncing the use of both negative numbers (as well as imaginary numbers), on the grounds that mathematicians were unable to explain their use except by physical analogies. [K, 678]

• Peacock, in his Treatise on Algebra, tackled the controversy about negative numbers by distinguishing between "arithmetical algebra" and "symbolical algebra". The former was arithmetic (of non-negative numbers) stated in general form by using letters rather than numbers. For example, in arithmetical algebra, a - b could be used, but only when b < a. In contrast, in symbolic algebra, the letters used as symbols need not have any interpretation. So, for example, a - b always made sense in symbolic algebra. Peacock defined a negative number as a symbol of the form -a. [K, 678-679]
• Hamilton, in his paper, "Theory of Conjugate Functions, or Algebraic Couples; with a Preliminary and Elementary Essay on Algebra as the Science of Pure Time," attempted to put negative numbers on a firm theoretical foundation (rather than the notion of quantities "less than nothing") by using the idea of "pure time" derived from Kant's Critique of Pure Reason. This attempt seems rather bizarre to us today, but it did help in the development of quaternions, the first example of an algebraic system that did not satisfy the commutative property for multiplication.[K, 682-684]

 References

[C] Cajori, Florian, History of Mathematics, 5th ed. Chelsea, New York, 1991

[K] Katz, Victor, A History of Mathematics: An Introduction, 2nd edition, Addison-Wesley, Reading, Mass., 1998

[Kl] Kline, Morris, Mathematical Thought form Ancient to Modern Times, Oxford University Press, New York, 1972

 [P] Parshall, Karen Hunger, The Art Of Algebra From Al-Khwarizmi To Viète: A Study In The Natural Selection Of Ideas, expanded version of an article in History of Science, Vol.26, No. 72, pp. 129 - 164, online at http://www.lib.virginia.edu/science/parshall/algebra.html

[Si] Sigler, L.E., Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation,  Springer, 2002.

 [S] Smith, David Eugene, History of Mathematics, v. II, Dover, New York, 1953
 
 

This page was prepared by Martha K. Smith, February 19, 2001