COMMON MISTEAKS MISTAKES IN USING STATISTICS: Spotting and Avoiding Them

Introduction   Types of Mistakes    Suggestions      Resources    Table of Contents  About   Glossary   Blog

Chart and Diagram for Confidence Interval Example

This chart and diagram may help clarify the terminology and ideas involved in understanding the concept of confidence interval.

The example: Y is a normal random variable; we are interested in a confidence interval for the mean µ of Y.
  Population One Simple Random Sample
y1, y2, ... , yn 		All Simple Random Samples of size n
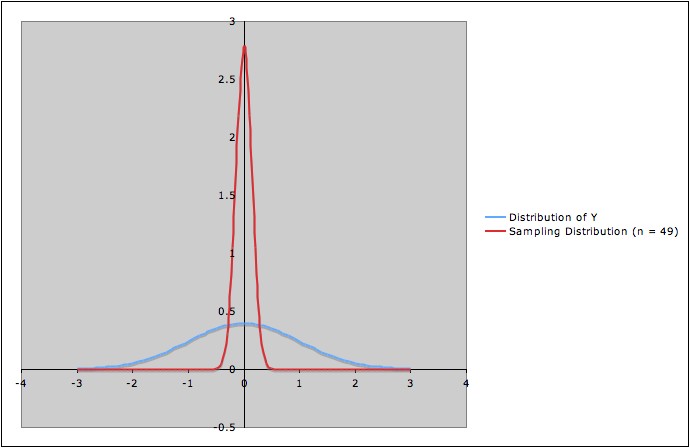
Associated Mean(s) Population mean µ, also called E(Y), or the expected value of Y, or the expectation of Y. Sample mean ȳ = (y1+ y2+ ... + yn)/n 1) Each sample has its own mean ȳ. This allows us to define a random variable Ȳn. The population for Ȳn is all simple random samples from Y. The value of Ȳn for a particular simple random sample is the sample mean ȳ for that sample.

2)  Since it is a random variable,   Ȳn also has a mean, E( Ȳn). Using the model assumptions  for this particular example, it can be proved that E( Ȳn) = µ. In other words, Y and Ȳn have the same mean as random variables.
Associated Distribution Distribution of Y None Sampling Distribution (Distribution of Ȳn )


The diagram shows the distribution of Y (in blue) and the sampling distribution (distribution of  Ȳn, in red) when Y is standard normal and n = 9. Notice that both distributions have the same mean.

Distribution of Y and sampling distribution of mean for samples of size n = 49 from Y
 
Last updated May 7, 2012