Using confidence intervals when prediction intervals are needed

As pointed out in the discussion of overfitting in regression, the model assumptions for least squares regression assume that the conditional mean function E(Y|X = x) has a certain form; the regression estimation procedure then produces a function of the specified form that estimates the true conditional mean function.

For example, if the model assumption is that
E(Y|X=x) = α +βx,
then least squares regression will produce an equation of the form
y = a +bx,
where a is an estimate of the true value α and b is an estimate of the true value β. Thus for a particular value of x,

ŷ = a +bx

is the estimate of E(Y|X = x).

But now suppose we want to estimate an actual value of Y when X = x, rather than just the conditional mean E(Y|X = x). The only estimate available for an actual value of Y is ŷ = a +bx, the same thing we used to estimate E(Y|X = x). But since Y is a random variable (whereas E(Y|X = x) is a single number, not a random variable), we cannot expect to estimate Y as precisely as we can estimate the conditional mean E(Y|X=x); i.e., even if ŷ is a good estimate of the conditional mean E(Y|X = x), it might be a very crude estimate of an actual value of Y.

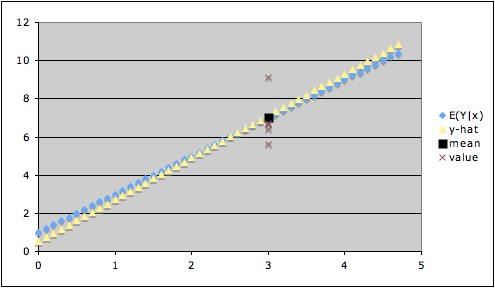
The graph below illustrates this. The blue line is the actual line of conditional means, the yellow line is the calculated regression line, the brown x's show some values of Y when x = 3, and the black square shows the value of the conditional mean of Y when x = 3. In this example, the estimate ŷ for x = 3 is virtually indistinguishable from the conditional mean when x = 3, so ŷ is a very good estimate of the conditional mean. But if we are trying to estimate Y when x = 3, our estimate ŷ (black square) might be way off -- for example, the value of Y might turn out to be at the highest brown x or at the lowest. This illustrates how the uncertainty of ŷ as an estimate of Y is much greater than the uncertainty of ŷ as an estimate of the conditional mean of Y.

Graph showing mean line, regression l ine, sample values at x = 3, and conditional mean at x = 3

To estimate the uncertainty in our estimate of the conditional mean E(Y|X = x), we can construct a confidence interval for the conditional mean. But, as we have seen, the uncertainty in our estimate of Y when X = x is greater than our uncertainty of E(Y|X = x). Thus, the confidence interval for the conditional mean underestimates the uncertainty in our use of ŷ as an estimate of a value of Y|(X = x). Instead, we need what is called a prediction interval, which takes into account the variability in the conditional distribution Y|(X = x) as well as the uncertainty in our estimate of the conditional mean E(Y|(X = x).

Example: With the data used to create the above plot, the 95% confidence interval for the conditional mean when x = 3 is (6.634, 7.568) (giving a margin of error of about 0.5) , and the 95% prediction interval for Y when x = 3 is (5.139, 9.062) (giving a margin of error of about 2) . (Note that the prediction interval includes all of the y-values associated with x = 3 in the data used, except for the highest one, which it misses by a hair.)

Comments:
1. For large enough sample size, the least squares estimate of the conditional mean is fairly robust to departures from the model assumption of normality of errors. This depends on the Central Limit theorem and the fact that the formula for ŷ can be expressed as a linear combination of the y-values for the data. However, since the t-statistic used in calculating the prediction interval also involves the conditional distribution directly, prediction is less robust to departures from normality.
2. The distinction between variability and uncertainty is useful in understanding the distinction between confidence intervals for the conditional mean and prediction intervals: The confidence interval for the conditional mean measures our degree of uncertainty in our estimate of the conditional mean; but the prediction interval must also take into account the variability in the conditional distribution¹.

Notes:
1. In fact, for least squares simple linear regression,

The width of the confidence interval depends on the variance of ŷ = ax + b as an estimator of E(Y|X = x),
whereas the width of the prediction interval depends on the variance of ŷ as an estimator of Y|(X = x).
The variance of ŷ as an estimator of Y|(X = x) is the sum of the conditional variance (usually denoted σ²) and the variance of ŷ as an estimator of E(Y|X = x).
The first term (σ²) is a measure of the variability in the conditional distribution;
the second term (the variance of ŷ as an estimator of E(Y|X = x)) is a measure of the uncertainty in the estimate of the conditional mean.
The conditional variance σ² typically is the larger of these two terms.