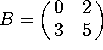 . Consider the linear transformations
. Consider the linear transformations
Problem 1.
Consider the vector space ![]() of
of ![]() matrices, let
matrices, let 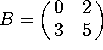 . Consider the linear transformations
. Consider the linear transformations ![]() and
and ![]() .
.
a) Find the matrix of ![]() relative to the basis
relative to the basis
![]()
We compute:
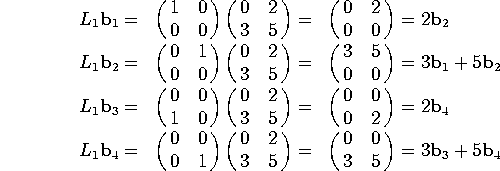
so we have
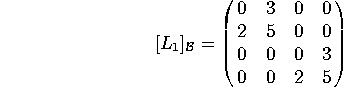
b) Find the matrix of ![]() relative to the same basis.
relative to the same basis.
We compute:
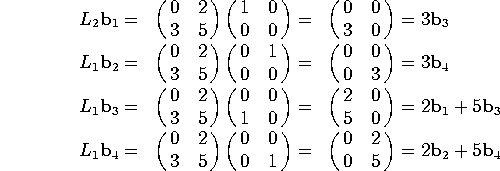
so we have
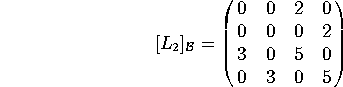
Problem 2. Let 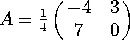 .
.
a) Consider the equations ![]() , with A as above. What are the stable and unstable modes? What
is the dominant eigenvector?
, with A as above. What are the stable and unstable modes? What
is the dominant eigenvector?
The eigenvalues are ![]() and
and ![]() , with eigenvectors
, with eigenvectors ![]() and
and ![]() . The first mode is stable since
. The first mode is stable since ![]() , while the second is unstable since
, while the second is unstable since ![]() . The dominant eigenvector is
. The dominant eigenvector is ![]() .
.
b) Consider the equations ![]() , with A as above. What are the stable and unstable modes? What
is the dominant eigenvector?
, with A as above. What are the stable and unstable modes? What
is the dominant eigenvector?
Now the question is whether the real part of ![]() is positive or negative. Since
is positive or negative. Since ![]() , the first mode is unstable. Since
, the first mode is unstable. Since ![]() , the second mode is stable. Now the dominant eigenvector is
, the second mode is stable. Now the dominant eigenvector is ![]() .
.
Problem 3. Let 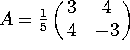 . Which of the following are Hermitian? Which are unitary? Which are both?
Which are neither?
. Which of the following are Hermitian? Which are unitary? Which are both?
Which are neither?
Notice that the eigenvalues of A are ![]() , and the eigenvectors are orthogonal. You can see this by calculating
them [they are
, and the eigenvectors are orthogonal. You can see this by calculating
them [they are ![]() and
and ![]() ], or from the fact that A is manifestly Hermitian. The various
operations all give matrices with the same eigenvectors as A, but
different eigenvalues. Since the eigenvectors are orthogonal, a matrix
will be Hermitian if its eigenvalues are real, and unitary if its eigenvalues
have norm one.
], or from the fact that A is manifestly Hermitian. The various
operations all give matrices with the same eigenvectors as A, but
different eigenvalues. Since the eigenvectors are orthogonal, a matrix
will be Hermitian if its eigenvalues are real, and unitary if its eigenvalues
have norm one.
a) A
Both Hermitian and unitary, since 1 and -1 are both real and of norm 1.
b) A + I
Hermitian but not unitary, since 2 and 0 are real but not of norm 1.
c) ![]()
Hermitian but not unitary, since ![]() are real but not of norm 1.
are real but not of norm 1.
d) ![]()
Unitary but not Hermitian, since ![]() are complex but of norm 1.
are complex but of norm 1.
Problem 4. In ![]() with the standard inner product, consider the vectors
with the standard inner product, consider the vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Apply Gram-Schmidt to turn this into an orthogonal basis for
. Apply Gram-Schmidt to turn this into an orthogonal basis for ![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
(sorry...that got cut off by the latex2html program. The final
answer is y4=(0,-1,1,0)^T.
Problem 5. Consider a sequence of numbers satisfying the second
order difference equation
x(n) = 2 x(n-1) +
3 x(n-2) for ![]() .
.
a) Reduce this 2nd order difference equation to a ![]() system of first order difference equations.
system of first order difference equations.
Let y(n)=x(n-1). Then x(n) = 2x(n-1) + 3y(n-1), and we have
![]()
b) Find the most general solution to the first order system.
The eigenvalues of the matrix are 3 and -1, with eigenvectors ![]() and
and ![]() , so the most general solution is
, so the most general solution is
![]()
c) From initial data x(0)=2, x(1)=2, find x(n) for all n.
We have 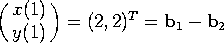 , so
, so ![]() and
and ![]() . Thus
. Thus ![]() .
.
Problem 6. Consider the nonlinear system of equations
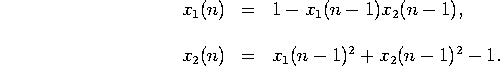
a) Linearize this system of equations near the fixed point ![]() .
.
![]()
Defining ![]() , our linearized equations are
, our linearized equations are ![]() .
.
b) Find the modes and determine which are stable and which are unstable.
The eigenvalues of A are ![]() , with eigenvectors
, with eigenvectors ![]() . Since both eigenvalues are (in magnitude) bigger than 1, both modes are
unstable.
. Since both eigenvalues are (in magnitude) bigger than 1, both modes are
unstable.
c) Is the fixed point ![]() stable?
stable?
And so ![]() is an unstable fixed point.
is an unstable fixed point.
Problem 7. Diagonalize the matrix 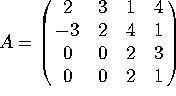
Since it is block triangular, to find the eigenvalues you just need
to diagonalize each block. The eigenvalues of the upper left block are ![]() , while the eigenvalues of the lower right block are 4 and -1. The eigenvectors
are
, while the eigenvalues of the lower right block are 4 and -1. The eigenvectors
are ![]() ,
, ![]() ,
, ![]() , b4=(1, 0, 1, -1)^T. Computing the first two entries of
, b4=(1, 0, 1, -1)^T. Computing the first two entries of ![]() is messy. I'll accept an answer of
is messy. I'll accept an answer of
(junk, junk, 3,2 ![]() .
.
Problem 8.
We wish to solve the differential equation
![]()
on the interval ![]() with Dirichlet boundary conditions:
with Dirichlet boundary conditions:
![]()
for all t. [This is called the Klein-Gordon equation, and comes up in relativistic quantum mechanics. We have not studied this equation, but you can solve it using the same ideas that gave us standing waves solutions to the wave equation.]
a) Find the eigenvalues and eigenfunctions of the operator ![]() (with Dirichlet boundary conditions).
(with Dirichlet boundary conditions).
We already know the eigenvalues and eigenvectors of ![]() , namely
, namely ![]() and
and ![]() . The eigenvalues of
. The eigenvalues of ![]() are just one less (
are just one less ( ![]() ) and the eigenvectors are the same.
) and the eigenvectors are the same.
b) Find the most general solution to (KG).
Let ![]() . Then
. Then
![]()
c) Given the initial conditions ![]() ,
, ![]() , find f(x,t) for all
, find f(x,t) for all ![]() and all t.
and all t.
The only nonzero coefficients are ![]() and
and ![]() , so
, so
![]()