Exam scores were pretty good. The class average was a 73;
the median was a 77. However, LOTS of people had trouble with exponentials
and logs. For instance, many people said that ln(x) could never be
negative. (You can't take the log of a negative number,
but ln(x)<0 whenever x<1). Another common mistake was forgetting
the rules for combining logs and writing something ln(2 e^2t) = 2(2t),
instead of ln(2) + 2t. A few people also wrote things like e^{-t}
+ e^{-2t} = e^{-3t}!
Exponentials and logs appear throughout M403L (and throughout mathematics). This is something you absolutely need to know.
Problem 1.
Consider the function ![]() . Note that this function is only defined for x>0.
. Note that this function is only defined for x>0.
a) Find the partition points of f and make a sign chart for f.
Since x is positive, the partition point is at ![]() , that is at
x=1. f(x) is positive for x>1
and negative for 0<x<1. A LOT of people mistakenly said that
f(x) was positive for 0<x<1.
, that is at
x=1. f(x) is positive for x>1
and negative for 0<x<1. A LOT of people mistakenly said that
f(x) was positive for 0<x<1.
b) Find the critical points of f and make a sign chart for f'.
![]() . This is zero when
. This is zero when ![]() , that is at x=1/e. f'(x) is negative for x<1/e
and positive for x>1/e. (A LOT of people said
that there were no critical points. This is simply wrong.)
, that is at x=1/e. f'(x) is negative for x<1/e
and positive for x>1/e. (A LOT of people said
that there were no critical points. This is simply wrong.)
c) Find the inflection points of f and make a sign chart for f''.
f''(x)=1/x is always positive. There are no inflection points.
d) Sketch the curve y=f(x). Mark all important
points CLEARLY. [You may find useful the fact that limit ![]() .]
.]
[Sorry, I can't do that online. But the curve starts at (0,0), heads downwards while curving upwards, reaches a minimum at (1/e, -1/e), crosses the x axis at (1,0), and continues to increase (and curve upwards) from then on.]
Problem 2.
Mariposa Ballot Services prints ballots for local governments. They have determined that demand for their ballots does not depend on the quality of their printing, but only on their price, via the relation p = 30 - 5 x, where x is the demand and p is the price. Their cost is C(x) = 10 + 10 x.
a) Compute the revenue function R(x) and the profit P(x).
![]() ,
, ![]() .
.
b) Compute the marginal revenue, the marginal cost, and the marginal profit as a function of x.
R'(x)=30-10x, C'(x)=10, and P'(x)=20-10x.
c) At what production level is the profit maximized? What is the profit at this level?
Where P'(x)=0, that is at x=2. The profit is P(2)=10.
d) At what production level is the revenue maximized?
Where R'(x)=0, namely at x=3. The revenue is R(3)=45. (You were not required to compute the revenue).
[Language note: Mariposa is Spanish for ``butterfly'']
Problem 3.
A homeowner wants his Christmas display to be as beautiful as possible. He has decided that a beautiful display should have both red and green lights. In fact, he considers the ``beauty index'' to be the product of the number of red and the number of green lights. If red lights cost $2 each and green lights cost $3 each, and if the homeowner has $60 to spend, how many lights of each type should he buy?
Let x be the number of red bulbs, and let y be the number
of green bulbs. We have 2x+3y=60, so y=20 - (2/3)x.
The beauty index is ![]() .
.
The maximum is when 0=B'(x) = 20 -4x/3, that is at x=15 and y=10. The homeowner should buy 15 red lights and 10 green lights.
You could just as well let y be the independent variable, and solve for x = (30 - 3y/2), so B= 30y - 3y^2/2. We then get 0=dB/dy = 30-3y, so y must be 10, and x=15.
Problem 4.
A Geiger counter is used to measure radioctivity. It clicks every time
the radiation from a decay hits it. In a particular experiment, it picks
clicks at a rate of ![]() .
.
a) At what time is the counter clicking fastest?
We want to maximize ![]() . We compute
. We compute ![]() and set it equal to zero, getting
and set it equal to zero, getting ![]() , or
, or ![]() .
.
b) How many clicks are recorded between time t=0 and time t=3?
![]()
Problem 5.
The price p and demand x for a commodity are related by
the equation ![]() . In particular, when p=10, x=30.
. In particular, when p=10, x=30.
a) Find dx/dp at the point (p,x)=(10,30).
Take the derivative of the equation with respect to p: ![]() , so
, so ![]() .
.
b) Use the result of part (a) to estimate the demand when the price is 10.1.
Use differentials. p=10, dp=.1, so dx=(dx/dp)
dp = -0.5, and ![]() .
.
Problem 6.
The marginal profit for a company is ![]() . Furthermore, the profit when x=10 is P(10)= 10,000. Find
the profit when x=2.
. Furthermore, the profit when x=10 is P(10)= 10,000. Find
the profit when x=2.
Integrate to get ![]() . Since P(10)=10,000, we must have C=-1000, so P(2)
= 2400 -8 -1000 = 1392.
. Since P(10)=10,000, we must have C=-1000, so P(2)
= 2400 -8 -1000 = 1392.
Part II:
Evaluate the following:
a) 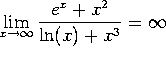 , since
, since ![]() grows faster than any other term.
grows faster than any other term.
b) 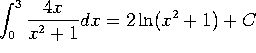 . This is an integration by substitution, with
. This is an integration by substitution, with ![]() .
.
c) 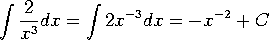 .
.
d) ![]() .
.
e) 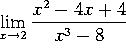 . Use L'Hopital's rule once to get
. Use L'Hopital's rule once to get ![]() .
.
f) 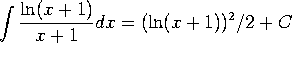 . This is an integration by substitution with
. This is an integration by substitution with ![]() .
.
g) 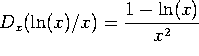 , by the ratio rule.
, by the ratio rule.
h) f''(x), where ![]() .
.
![]() , and
, and ![]() .
.
i) 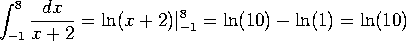 .
.
j) 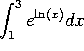 . Since
. Since ![]() , this is just
, this is just ![]()