This is an actual M403K midterm given on September 22, 1992. On that test I allowed a ``crib sheet'' and a non-graphing calculator.
The syllabus has changed some in 8 years, so this exam doesn't cover exactly the same material as our first midterm will. In particular, problem 4 is Chapter 2 material, which will be tested in the second midterm.
Problem 1. Tangent lines
Consider the curve
![]()
a) Find dy/dx when x=1.
b) Find the slope of the line that is tangent to this curve at the point (1,4).
c) Find the equation of this line.
Problem 2. Derivatives and limits
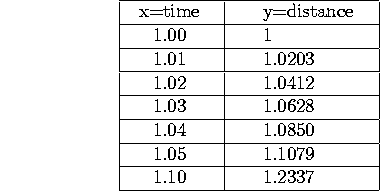
A race car driver is circling the track at Indianapolis. The table below gives his position at various times (x denotes time, in hours. y denotes distance, in miles).
How fast is he going at time x=1?
Problem 3. Limits and continuity
Consider the function
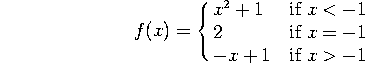
a) Find the limit of f(x) as x approaches -1 from below, as x approaches
-1 from above, and the overall limit ![]() , if they exist.
, if they exist.
b) Is f(x) continuous at x=-1? Why or why not?
Problem 4. Graphs and optimization
Consider the function ![]() .
.
a) Find all the partition points of f. For what values of x is f(x) positive?
b) Find all the critical points of f. For what values of x is f(x) increasing?
c) Find all the local minima of f(x).
Problem 5. Taking derivatives
Take the derivatives, with respect to x, of the following functions. You do NOT need to simplify your results:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
Problem 6. Taking limits
Evaluate the following limits:
a)
![]()
b)
![]()
c)
![]()
d)
![]()