This exam consists of 2 parts. Part I contains 10 short ``grab-bag''
questions, each worth 4 points. Part II contains 5 longer problems,
each worth 12 points.
This test is CLOSED BOOK. However, each student is allowed to bring
two ![]() by 11 sheets of prepared notes into the test. Other than
these sheets, you are only allowed your pencils and pens and a
NON-GRAPHICS calculator.
by 11 sheets of prepared notes into the test. Other than
these sheets, you are only allowed your pencils and pens and a
NON-GRAPHICS calculator.
Evaluate the following derivatives, integrals, and limits, and simplify the following expressions involving exponentials and logs.
For problems A-D, you do NOT have to reduce your answers to the simplest possible forms. Any correct answers will do.
However, for problems E-J, I do want answers in the simplest possible form. For example, if the answer is zero, then writing ``ln(1)'' (which DOES equal zero, of course) will only get you partial credit. Also, you should show your reasoning. Just pulling numbers from a calculator will get you NO credit.
Some of the limits may not exist. If they don't exist, write ``DNE'' or ``does not exist'' in the box.
A. Find F(x), where ![]() and F(0)=5.
and F(0)=5.
Integrate by substitution with ![]() ,
, ![]() .
.
![]() .
Since F(0)=5, C must equal 4, so
.
Since F(0)=5, C must equal 4, so ![]() .
.
B. Evaluate: 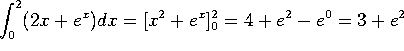 .
.
C. Find f'(x), where ![]() .
.
![]() .
.
D. Find f'(x), where ![]() and
and ![]() .
.
![]() .
.
E. Find f'(x), where 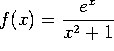
Ratio rule: 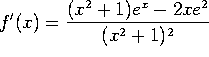
F. Evaluate (and simplify): 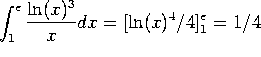 . (This was integration by
substitution, with
. (This was integration by
substitution, with ![]() .)
.)
G. Evaluate (and simplify):
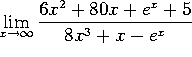
Apply L'Hopital's rule four times to get ![]() . Either that
or recognize that exponentials beat polynomials, so that the only important
terms are the
. Either that
or recognize that exponentials beat polynomials, so that the only important
terms are the ![]() 's in the numberator and denominator.
's in the numberator and denominator.
H. Evaluate (and simplify):
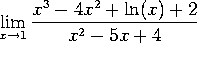
Plugging in x=1 gives -1/0. This is NOT a L'Hopital's rule problem. The limit does not exist!
I. Simplify: ![]() .
.
J. Simplify: ![]()
This part consists of 5 longer problems, each worth 12 points.
Problem 1. A certain professor of mathematics overeats during a 12-day holiday period and gains weight. The rate at which he gains weight is given by the formula:
![]()
where his weight, W(t), is measured in pounds, and the time t is measured in days. (That is, the holiday starts at t=0 and ends at t=12).
Note that parts (a) and (b) below can be done independently of each other. Part (a) involves differentiation, while part (b) involves integration.
a) At what time is the professor gaining weight the fasting? How fast is he gaining at that time?
To maximize W'(t), set the derivative of W'(t) to zero, so 0 = (8-2t)/48, so t=4. At that time he is gaining weight at a rate of W'(4)= 64/48 = 4/3 pounds per day.
b) If he starts the holidays weighing 160 pounds, what is his weight at the end of the holidays?
![]() . Since W(0)=160,
we must have C=160. Then W(12) = 12 + 12 - 12 + 160 = 172.
. Since W(0)=160,
we must have C=160. Then W(12) = 12 + 12 - 12 + 160 = 172.
Problem 2. Consider the function ![]() .
.
a) Find all the partition points of f. For what values of x is f(x) positive? Find all the horizontal asymptotes (if any) and all the vertical asymptotes (if any).
The only partition point is at x=0. Since ![]() is always positive,
f(x) is positive for x;SPMgt;0 and negative for x;SPMlt;0. There is a horizontal
asymptote on the left at y=0, since
is always positive,
f(x) is positive for x;SPMgt;0 and negative for x;SPMlt;0. There is a horizontal
asymptote on the left at y=0, since ![]() , but
there is no horizontal asymptote on the right. There are no vertical
asymptotes.
, but
there is no horizontal asymptote on the right. There are no vertical
asymptotes.
b) Compute f'(x). Find all the critical points, and for each one say whether it is a local minimum, a local maximum, or neither. For what values of x is f increasing?
![]() . The only critical point is at x=-1/2. f(x) is
increasing for x;SPMgt;-1/2 and decreasing for x;SPMlt;-1/2.
. The only critical point is at x=-1/2. f(x) is
increasing for x;SPMgt;-1/2 and decreasing for x;SPMlt;-1/2.
c) Compute f''(x). Find all the points of inflection. For what values of x is the graph of f concave up?
![]() . The only point of inflection is at x=-1.
The graph is concave up for x;SPMgt;-1 and concave down for x;SPMlt;-1.
. The only point of inflection is at x=-1.
The graph is concave up for x;SPMgt;-1 and concave down for x;SPMlt;-1.
d) Sketch the graph of f(x).
Sorry, but I can't do that on-screen.
Problem 3. Suppose that a colony of bacteria is growing in your lungs (cough, cough). The number of bacteria, N(t), is growing according to the formula
![]()
where t is time, measured in hours. At midnight (t=0) there are 10 bacteria in your lungs (i.e. N(0)=10).
a) How many bacteria will there be at time t? (This answer should be a formula)
![]() .
.
b) How many will there be at 8 AM? (This answer should be a number)
![]() 88 million.
88 million.
c) At what time will there be 1000 bacteria?
![]() , so
, so ![]() , so
, so ![]() ,
so
,
so ![]() . That is, around 2:18 AM.
. That is, around 2:18 AM.
4. a) Consider the curve ![]() . Find dy/dx at the
point (10,1).
. Find dy/dx at the
point (10,1).
![]() , so
, so ![]() .
.
b) The pressure and volume of gas in a piston are related by the
formula ![]() , where p denotes pressure and V denotes volume.
When p=10 and V=1, the volume is increasing at a rate of dV/dt=2.
At what rate is the pressure changing?
, where p denotes pressure and V denotes volume.
When p=10 and V=1, the volume is increasing at a rate of dV/dt=2.
At what rate is the pressure changing?
This is almost the same problem. ![]() , so
, so
![]()
5. Let ![]() . Let
. Let ![]() .
.
a) Where do the curves y=f(x) and y=g(x) meet?
![]() , so
, so ![]() , so 2(x)(x-5)=0, so x=0 or
x=5.
, so 2(x)(x-5)=0, so x=0 or
x=5.
b) Find the area between the two curves.
![]() .
.