1. An explosive shell is shot out of a cannon. Its height above the
ground (in feet) is given by the function ![]() , where x is the time (in seconds) since the firing.
, where x is the time (in seconds) since the firing.
a) Find the velocity of the shell as a function of time.
f'(x) = 160 - 32 x.
b) What is the shell's velocity at time x=4? At that time, is it heading up or down?
f'(4) = 160 - 4(32) = 32. That is, the shell's height is increasing at 32 feet/second, which means it is still heading up.
c) The shell will hit the ground again at time x=10. What will its velocity be at that time?
f'(10) = 160 - 10(32) = -160. This velocity is negative, meaning the shell is falling at 160 feet/second.
2. a) From the following table, estimate f'(3). Indicate clearly how you obtain your answer:

Compute [f(3+h)-f(3)]/h for different values
of h, and take the limit as ![]() .
.
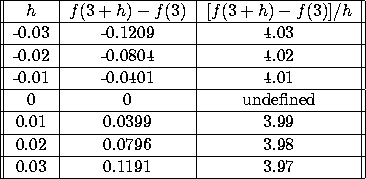
It's clear that the limit as ![]() is 4. So f'(3)=4.
is 4. So f'(3)=4.
b) You receive a secret message saying that the function in part (a)
was really ![]() . If this message is true, what should f'(3) equal? How does
this compare to the answer you got in part (a)?
. If this message is true, what should f'(3) equal? How does
this compare to the answer you got in part (a)?
If the message is true, then ![]() , so
f'(3)=4, in agreement with the answer to part (a). In fact,
the function in part (a) really is
, so
f'(3)=4, in agreement with the answer to part (a). In fact,
the function in part (a) really is![]() , tabulated to 4 decimal places.
, tabulated to 4 decimal places.
3. Evaluate the following limits, if they exist (or write DNE if they do not).
a) 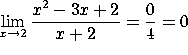
b) 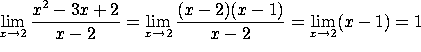
c) 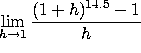 . TYPO ALERT!! I had intended this to be a question about
the h => 0 limit. The h=>0 limit is the derivative of the function
. TYPO ALERT!! I had intended this to be a question about
the h => 0 limit. The h=>0 limit is the derivative of the function ![]() at x=1. Since
at x=1. Since ![]() , that limit would be f'(1)=14.5. As h => 1, however, neither
the numerator nor the denominator goes to zero, so we can just plug in
h=1 to get [2^(14.5) - 1]. In grading, I will accept a calculation
of either limit, as long as it is done correctly.
, that limit would be f'(1)=14.5. As h => 1, however, neither
the numerator nor the denominator goes to zero, so we can just plug in
h=1 to get [2^(14.5) - 1]. In grading, I will accept a calculation
of either limit, as long as it is done correctly.
d) ![]() . The numerator approaches 5, while the denominator approaches zero from
the negative side, so the ratio goes to
. The numerator approaches 5, while the denominator approaches zero from
the negative side, so the ratio goes to ![]() . I will also accept the answer "does not exist".
. I will also accept the answer "does not exist".
4. Take the derivatives of the following functions with respect to x. You do not need to simplify your answers:
a) ![]() .
.
By the chain rule, ![]() .
.
b) ![]() . By the product rule,
. By the product rule, ![]() .
.
c) ![]()
By the ratio rule, ![]()
d) ![]()
Combining the product rule and the chain rule, we get ![]() .
.
5. Nimbus Racing Brooms, Ltd. has just released their finest model, the Nimbus 2002. (Available at Quality Quiddich Supplies and fine stores everywhere.) Their marketing department has determined that the demand function is x = 800 - 40p, where x is the number of brooms sold (per month) and p is the price (in gold galleons). The cost function is C(x)= 500 + 10x.
a) Find the price p(x) and the revenue R(x) as a function of x.
Solving for p gives ![]() , so
, so ![]() .
.
b) Compute the marginal cost, marginal revenue and marginal profit as a function of x.
C'(x) = 10, ![]() , and
, and ![]() .
.
c) The factory is currently producing x=300 brooms/month. To increase revenue, should the company increase or decrease production?
When x=300, ![]() , so each additional broom will increase revenue by 5 galleons.
To increase revenue, the company should increase production.
, so each additional broom will increase revenue by 5 galleons.
To increase revenue, the company should increase production.
d) Likewise, if the company wants to increase profit, should it increase or decrease production?
When x=300, ![]() , so each additional broom will decrease profits by 5 galleons.
To increase profits, decrease production!
, so each additional broom will decrease profits by 5 galleons.
To increase profits, decrease production!