M328K Final Exam Solutions, May 10, 2003


1. ``Bibonacci'' numbers. The Bibonacci numbers tex2html_wrap_inline76 are defined by tex2html_wrap_inline78 , tex2html_wrap_inline80 , and, for n>2, tex2html_wrap_inline84 .

a) Prove that, for all positive integers n, tex2html_wrap_inline88 .

The proof is by generalized induction. It is true for n=1 and n=2. Now suppose it is true for all n up to k-1. Then tex2html_wrap_inline98 and tex2html_wrap_inline100 , so tex2html_wrap_inline102 .

b) Prove that, for all positive integers n, tex2html_wrap_inline106 .

The proof is also by generalized induction. It is true for n=1 and n=2. Now suppose it is true for all n up to k-1. Then tex2html_wrap_inline116 and tex2html_wrap_inline118 , so tex2html_wrap_inline120 . 

Note: The exact formula works out to tex2html_wrap_inline122 , which also can be proven by induction.

2. The following theorem-proof combination is erroneous. Find the errors (there are at least two). Then, rewrite the proof (and, if necessary, the statement of the theorem) so that it really does prove the theorem.

``Theorem'' Every positive integer is divisible by a prime.

``Proof'' Let n be a positive integer. If n is prime, then n is divisible by the prime n, and we are done. If n is composite, then n = ab, where a and b are integers less than n. If a is prime, then a|n, and we are done. If a is composite, write a as a product of two smaller integers, and examine the first of these. Repeat this process, dividing composite factors into products of still smaller factors, and examining the first sub-factor, until you get a factor that cannot be divided further, and is therefore prime.

The first error is that not all positive integers are prime or composite. The integer 1 is neither prime nor composite, and if n is equal to 1, then n isn't divisible by a prime. The second error is that we never show that the process of dividing into factors ever stops. Why can't you keep dividing into smaller factors forever without reaching a prime? The answer requires the Well-Ordering Principle.

Here is a corrected theorem, and two versions of the corrected proof, one using induction and the other using the well-ordering principle directly:

Theorem Every integer greater than 1 is divisible by a prime.

Proof 1 We prove this by induction. It is true for n=2, since 2|2. Now suppose it is true for all n from 2 to k-1. We must show that k is divisible by a prime. If k is prime, then k is divisible by the prime k, and we are done. If k is not prime, it must be composite, since k;SPMgt;1. Thus k=ab, where a and b are integers less than k and greater than 1. By the inductive hypothesis, a is divisible by a prime p, hence k is also divisible by p.

Proof 2 Let n be a positive integer greater than one. If n is prime, then n is divisible by the prime n, and we are done. If n is composite, then tex2html_wrap_inline200 , where tex2html_wrap_inline202 and tex2html_wrap_inline204 are integers less than n. If tex2html_wrap_inline202 is prime, then tex2html_wrap_inline210 , and we are done. If tex2html_wrap_inline202 is composite, write tex2html_wrap_inline214 as a product of two integers, each bigger than 1 and smaller than tex2html_wrap_inline202 , and examine the first factor tex2html_wrap_inline218 . Repeat this process, dividing composite factors into products of still smaller factors, and examining the first sub-factor. The set tex2html_wrap_inline220 is nonempty. By the Well-Ordering Principle, this set has a smallest elements tex2html_wrap_inline222 . This implies that tex2html_wrap_inline222 is prime, for if tex2html_wrap_inline222 were composite, tex2html_wrap_inline228 would exist and would be smaller than tex2html_wrap_inline222 . Since tex2html_wrap_inline232 , n is divisible by a prime.

3. Matrix products. It is a known fact that, if A and B are matrices such that the product AB makes sense, then tex2html_wrap_inline242 . (That is, the transpose of the product is the product of the transposes, in the opposite order). Taking this fact as given, prove the following statement:

Claim: Let n;SPMgt;1 and let tex2html_wrap_inline246 be an ordered n-tuple of matrices such that the product tex2html_wrap_inline250 is defined. Then tex2html_wrap_inline252 , i.e., the transpose of the product is the product of the transposes with the order reversed.

This is yet another proof by induction on n. (In this case it is regular induction, not generalized induction). The base case is n=2, which is given. Now suppose it is true for n=k-1. Then tex2html_wrap_inline260 . Take tex2html_wrap_inline262 and tex2html_wrap_inline264 . Then tex2html_wrap_inline266 .

4. a) Find the greatest common factor of 50 and 76.

b) Write this number as a linear combination of 50 and 76.

Use the Euclidean algorithm:

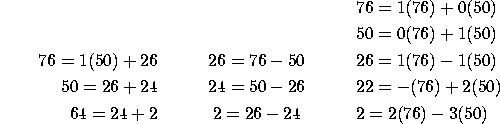
eqnarray44

So (50,76)=2=2(76)-3(50)

c) Find all solutions, mod 76, of the equation tex2html_wrap_inline270 .

Since (-3)50 = 2 (mod 76), we must have -27 (50) = 18 (mod 76). The solution is only defined mod 76/(76,50) = 38, so the solutions mod 76 are 11 and 49.

5. a) Find all solutions, in the range tex2html_wrap_inline278 , to the following system of congruences.

eqnarray47

Use the Euclidean argument to get that 1 = 4(49) - 13(15) = 196 - 195. A solution is therefore tex2html_wrap_inline282 (mod 735).

b) Find all solutions, in the range tex2html_wrap_inline284 , to the system of congruences

eqnarray51

Use the Euclidean algorithm on the first two equations to get x=33 (mod 35). Combine that with the third equation to get x=68 (mod 385). Combine that with the last equation to get x=838 (mod 5005).

6. a) Compute tex2html_wrap_inline292 (mod 101). (Note that 101 is prime)

Since tex2html_wrap_inline294 , we only care about 883 (mod 100), so we can take the 83rd power instead of the 883rd. By successive squaring (and reduction mod 101), we have tex2html_wrap_inline296 , tex2html_wrap_inline298 , tex2html_wrap_inline300 , tex2html_wrap_inline302 , tex2html_wrap_inline304 , tex2html_wrap_inline306 , and tex2html_wrap_inline308 . Then tex2html_wrap_inline310

b) You are told that tex2html_wrap_inline312 (mod 101) and that tex2html_wrap_inline314 . Find a positive integer d such that tex2html_wrap_inline318 .

We seek an inverse to 83 (mod 100). By the Euclidean algorithm (again!) we get tex2html_wrap_inline320 (note that tex2html_wrap_inline322 .) So d=47.

c) If y=24, what is x? By successive squaring, we get tex2html_wrap_inline330 . You can check directly, again by successive squaring, that tex2html_wrap_inline332 .

7. Let n=8999271. a) What is the prime factorization of n? (Hint: n is the product of more than two primes) You may use your calculators, but you may NOT use a ``factor'' key or function, and you MUST show how you did the factorization in order to receive credit.

It's clear that 9|n, so we factor that out to get n=9m, where m=999919. Using Fermat's method we see that this is tex2html_wrap_inline346 . Both 991 and 1009 are prime, so our factorization is tex2html_wrap_inline348

b) Compute tex2html_wrap_inline350 .

tex2html_wrap_inline352 .

c) Somebody suggests coding numbers by tex2html_wrap_inline354 , where x is relatively prime to n. Find a key that decodes this (i.e., a number k such that tex2html_wrap_inline362 .

By the Euclidean argument, tex2html_wrap_inline364 , so tex2html_wrap_inline366 , so our answer is -352207 (mod tex2html_wrap_inline350 ). The smallest positive representative is tex2html_wrap_inline372 .

[In fact, the smaller key k' = 55440 will also work. 17 k' isn't equal to 1 mod tex2html_wrap_inline350 , but it is equal to 1 mod the least common multiple of 990, 1008 and 6, so taking things to the 17k' power preserves their residue class mod 9, mod 991, and mod 1009, and hence mod n.]


Lorenzo Sadun
Sat May 10 20:35:43 CDT 2003