![]()
We prove this by induction. The formula is true for the base case n=1,
since ![]() Now for the inductive step. We assume the formula is true for n=m-1
and show it works for n=m. If it is true for n=m-1,
then
Now for the inductive step. We assume the formula is true for n=m-1
and show it works for n=m. If it is true for n=m-1,
then
![]()
But then
![]()
which is the formula we needed to show.
2. As you know, the Fibonacci numbers ![]() are defined by
are defined by ![]() ,
, ![]() and, for n>2,
and, for n>2, ![]() . Give a rigorous proof of the assertion: ``
. Give a rigorous proof of the assertion: `` ![]() is divisible by 3 if and only if n is divisible by 4.'' [Hint:
Before writing down your proof, you may want to first determine which Fibonacci
numbers are congruent to 1 (mod 3), which are congruent to 2 (mod 3), and
which are divisible by 3. I'm sure you'll see the patters quickly enough.]
is divisible by 3 if and only if n is divisible by 4.'' [Hint:
Before writing down your proof, you may want to first determine which Fibonacci
numbers are congruent to 1 (mod 3), which are congruent to 2 (mod 3), and
which are divisible by 3. I'm sure you'll see the patters quickly enough.]
I claim that
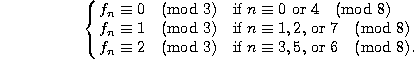
If we can prove this, then the original assertion follows, since being divisible by 4 is the same as being congruent to 0 or 4 modulo 8.
We prove the claim by (generalized) induction. It is true for the base
cases n=1 and n=2, since ![]() . Now, for m;SPMgt;2, suppose that it is true for all values
of n up to m-1. We must show it is true for n=m.
There are 8 cases to check:
. Now, for m;SPMgt;2, suppose that it is true for all values
of n up to m-1. We must show it is true for n=m.
There are 8 cases to check:
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() and
and ![]() , so
, so ![]() .
.
Similarly, if ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
If ![]() , then
, then ![]() and
and ![]() , so
, so ![]() , and then we're done.
, and then we're done.
3. Greatest common factors:
a) Find the greatest common factor of 66 and 52.
By the Euclidean algorithm: 66 = 1(52) + 14; 52 = 3(14) + 10; 14 = 1(10)+4; 10 = 2(4) + 2; 4 = 2(2). So (66,52)=2.
b) Write this number explicitly as a linear combination of 66 and 52.
For instance, if (66,52) were equal to 24 (which it obviously isn't!), you
might write `` ![]() ''.
''.
Working through the algorithm, we have 14 = 66 - 52; 10 = 52 - 3(14) = 4(52) - 3(66); 4 = 14 - 10 = 4(66) - 5(52); and finally our answer: 2 = 10 - 2(4) = 14(52) - 11(66).
c) What is the least common multiple of 66 and 52?
![]() .
.
4. Congruences, Diophantine equations and the Chinese Remainder Theorem.
a) Find all integer solutions to the equation 25 x + 38 y = 1.
By inspection, or by the Euclidean algorithm, you can see that -3(25) + 2(38) = -75 + 76 = 1. Thus ALL integer solutions are of the form
![]()
where n is an arbitrary integer.
b) Find a solution to the equation ![]() .
.
This is the same question, and the answer is x=-3 (or x=35, or any number that is congruent to -3 modulo 38).
c) Find a solution to the equation ![]() .
.
There was a typo in the question. It should have read "mod 25", not "mod 28". As written, there is no answer, since the left hand side is always congruent to 0 (mod 38). As intended, the answer is x=2 (or anything congruent to 2 modulo 25).
d) Find a positive solution to the congruences ![]() ,
, ![]() .
.
Since ![]() and
and ![]() , and since
, and since ![]() and
and ![]() , x=5(76)+8(-75) = -220 is congruent to 5 modulo 25 and 8 modulo
38. However, we wanted a POSITIVE solution, so we add an arbitrary multiple
of (25)(38)=950. The smallest solution is -220+950 = 730.
, x=5(76)+8(-75) = -220 is congruent to 5 modulo 25 and 8 modulo
38. However, we wanted a POSITIVE solution, so we add an arbitrary multiple
of (25)(38)=950. The smallest solution is -220+950 = 730.
Lorenzo Sadun