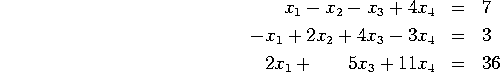
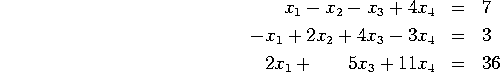
Is the set of solutions empty, a point, a line, a plane, or some other geometric shape? If it is a line or a plane, express this set in parametric form.
2. Consider the matrix and vector
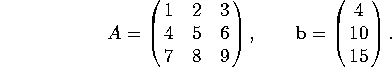
a) Is 
in the span of the columns of A? If so, write
explicitly as a linear combinations of the columns.
b) Are the columns of A linearly independent? If not, write the zero vector as a nontrivial linear combination of the columns of A.
3. Consider the linear transformation 
given by
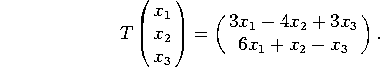
a) Find the matrix of T.
b) Is T one-to-one? Why or why not?
c) Is T onto? Why or why not?
4. Indicate whether each of these matrices is invertible. If it is, find the inverse. If it isn't invertible, explain why.
a)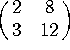 
b)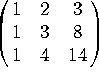 
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The columns of a 
matrix must be linearly dependent.
b) The columns of a
matrix must span 
.
c) If two matrices A and B have different sizes, then the sum A + B is not defined.
d) If two matrices A and B have different sizes, then the product AB is not defined.
e) If A and B are inverses, then AB=BA.
f) If a set 
of 2 or more vectors is linearly dependent, then one of the vectors is
a linear combination of the others.
g) If the columns of a 
matrix are linearly independent, then they span
.
h) If the columns of an 
matrix are linearly independent, then they span 
.
i) If a 
matrix A has exactly 3 pivots, then the linear transformation 
is one-to-one.
j) If a
matrix A has exactly 3 pivots, then the linear transformation
is onto
Lorenzo Sadun