1. The following two ![]() matrices are row-equivalent:
matrices are row-equivalent:
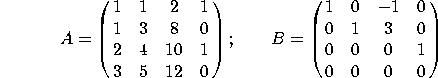
a) What is the rank of A?
b) Find a basis for the column space of A.
c) Find a basis for the null space of A.
d) Find a basis for the row space of A.
2. Let V=Span 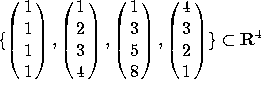 .
.
a) What is the dimension of V?
b) Find a basis for V.
c) Let W be the subspace of ![]() spanned by the polynomials
spanned by the polynomials ![]() ,
, ![]() ,
, ![]() and
and ![]() . What is the dimension of W? Find a basis for W.
. What is the dimension of W? Find a basis for W.
3. Consider the following basis for ![]() :
:
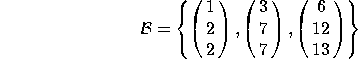
a) Find the change-of-basis matrix ![]() that converts from coordinates in the B basis to coordinates in
the standard (E) basis.
that converts from coordinates in the B basis to coordinates in
the standard (E) basis.
b) Fina the change-of-basis matrix ![]() that converts from coordinates in the standard basis to coordinates in
the B basis.
that converts from coordinates in the standard basis to coordinates in
the B basis.
c) Let 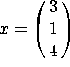 . Compute
. Compute ![]() .
.
d) Consider the basis ![]() ,
, ![]() ,
, ![]() for the vector space
for the vector space ![]() . Find the coordinates of the polynomial
. Find the coordinates of the polynomial ![]() in this basis.
in this basis.
4. a) Are the polynomials ![]() ,
, ![]() and
and ![]() linearly independent?
linearly independent?
b) Do the polynomials ![]() ,
, ![]() and
and ![]() span
span ![]() ?
?
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The rank of a matrix is the dimension of its row space.
b) Let ![]() be vectors in a vector space V. For Span
be vectors in a vector space V. For Span ![]() to be a subspace of V, the vectors must be linearly independent.
to be a subspace of V, the vectors must be linearly independent.
c) If A and B are row-equivalent matrices, then Col(A)=Col(B).
d) If A and B are row-equivalent matrices, then Null(A)=Null(B).
e) If A and B are row-equivalent matrices, then Row(A)=Row(B).
f) Let ![]() be a collection of four vectors in
be a collection of four vectors in ![]() . One of the
. One of the ![]() 's can be written as a linear combination of the others.
's can be written as a linear combination of the others.
g) If a collection of five polynomials spans ![]() , then it forms a basis for
, then it forms a basis for ![]() .
.
h) Every change-of-basis matrix is invertible.
i) If a linearly dependent set of vectors spans ![]() , then there must be at least 4 vectors in the set.
, then there must be at least 4 vectors in the set.
j) If ![]() is a linearly independent set of vectors in V, and
is a linearly independent set of vectors in V, and ![]() is a spanning set for V, then n>k.
is a spanning set for V, then n>k.