L(p(t)) = (t+1)p'(t) - 2p(t). As usual,
Problem 1: Consider the linear operator ![]() ,
,
L(p(t)) = (t+1)p'(t) - 2p(t).
As usual, ![]() is the space of 2nd order polynomials in the variable t.
is the space of 2nd order polynomials in the variable t.
a) What is the matrix of L relative to the basis ![]() ?
?
b) Find the dimension of the kernel of L and the dimension of the range of L.
c) Find a basis for the kernel of L. Also, find a basis for the range of L.
Problem 2 This problem concerns changing bases in ![]() . Let S be the standard basis. Let
. Let S be the standard basis. Let ![]() be another basis, where
be another basis, where ![]() ,
, ![]() ,
, ![]() .
.
a) Find a matrix P that converts from the T basis to the
S basis. That is, so that for any vector X, ![]() .
.
b) Find a matrix Q that converts from the S basis to the
T basis. That is, so that for any vector X, ![]() .
.
c) There is a linear operator L whose matrix, relative to the
S basis, is 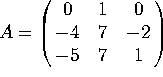 . Find the matrix of L relative to the T basis.
. Find the matrix of L relative to the T basis.
Problem 3. Let 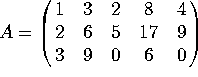
a) What is the rank of A?
b) Find a basis for the null space of A.
c) Find a basis for the row space of A.
Problem 4. Let V be the span of ![]() and
and ![]() , where
, where ![]() ,
, ![]() and
and ![]() .
.
a) Find an orthogonal basis for V.
b) Find an orthonormal basis for V.
Problem 5. True of False
a) The map ![]() , L(x,y)=(x+y,y-1), is a linear
transformation.
, L(x,y)=(x+y,y-1), is a linear
transformation.
b) The map ![]() ,
, ![]() , is a linear transformation.
, is a linear transformation.
c) The map ![]() , L(x,y)=(3 x+ y,y-5x),
is a linear transformation.
, L(x,y)=(3 x+ y,y-5x),
is a linear transformation.
d) Let L be a linear transformation from ![]() to
to ![]() . If the rank of L is 3, then the kernel of L is 1-dimensional.
. If the rank of L is 3, then the kernel of L is 1-dimensional.
e) Let L be a linear transformation from ![]() to
to ![]() . If the kernel of L is 2 dimensional, then L is onto.
. If the kernel of L is 2 dimensional, then L is onto.
f) Let L be a linear transformation from ![]() to
to ![]() . If L is 1-1, then L is onto.
. If L is 1-1, then L is onto.
g) If a set of vectors is orthonormal, then it is a basis.
h) If a set of vectors is orthonormal, then it is linearly independent.
i) If a matrix is wider than it is tall (e.g. a ![]() matrix), then the row rank is greater than the column rank.
matrix), then the row rank is greater than the column rank.
j) Let L be a linear transformation from ![]() to itself. The solutions (in
to itself. The solutions (in ![]() ) to the equation L(p)=0 form a vector space.
) to the equation L(p)=0 form a vector space.