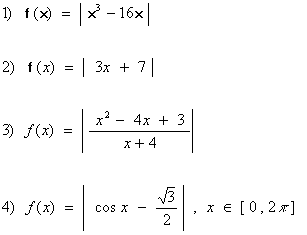M 408 C  Spring 2002     HW #6, Part II:   Piece-wise Defined  Formulas the Absolute Value of Functions

In each of the problems below, a function  f(x) is defined using the absolute value function in its formula.  The assignment is to determine a piece-wise defined formula for f(x) which does not involve the absolute value function.

The method for developing this piece-wise defined formula can be described as follows:

          1) Write  u  for the expression contained in the absolute value signs.

          2)  Solve for the values of  x  such that   u  =  0   or   such that  u  is undefined (as from division by 0).

          3)  List the open intervals (a,b) of real numbers which have the x-values found in Step 2 as endpoints.

          4)  Test each interval formed in Step 3 by selecting a number for x in that interval and determining the value of u there.  If  u < 0 at that selected number x, then u < 0 at every value of x in the interval.

          5)  If  u < 0 on an interval, the piece-wise defined formula will have  |u| = - u  for x in that interval.  If  u > 0 on an interval, the piece-wise defined formula will have  |u| = + u  for x in that interval .

          6) After the formula for f(x) has been constructed for all the intervals formed in Step 4, the piece-wise definition must be extended appropriately to include those values of x for which  u = 0.  Since both formulas, +u and –u, will evaluate to 0 at these values of x, either can be used to define  f(x) at these values of x.

An Example of using the solution method described above follows:

    Example Problem (with solution):

         For the given function  f(x), determine a piece-wise defined formula for f(x) which does not involve the absolute value function.

           The given function:      .

Step 1)    .   

Step 2)    u = 0:  ( x + 7 ) ( x – 10 )  =  0  ;   x  =  -7 ,  10 ;  u is undefined for  x = 15 .

Step 3)  Intervals:  (  –infinity, -7 ) ; (  –7, 10 )  ;  ( 10, 15 )  ;  ( 15, infinity )

Steps 4 and 5:

               Test ( –infinty,  –7 ) :  x  <  –7 .

                   At  x  =  –10 ,  u  =  –12/5  <  0 ;  |u|  =  –u  .

              Test ( –7, 10 ) :   –7  <  x  <  10 .

                   At  x  =  2 ,  u  =  72/13  >  0 ;  |u|  =  +u  .

               Test ( 10,  15 ) :   10  <  x  <  15 .

                   At  x  =  12 ,  u  =  –38/3  <  0 ;  |u|  =  –u  .

              Test ( 15, +infinity ) :   x   >   15 . 

                   At  x  =  20 ,  u  =  54  >  0 ;  |u|  =  +u  .

Step 6:  Since u = 0 at both x = -7 and at x = 10, extend the use of  the |u| =  +u formula from ( -7, 10) to the closed interval [ -7, 10] .  Since  u is not defined at x = 15, do not include x = 15 in the domain of definition of f(x).

    Final Solution:

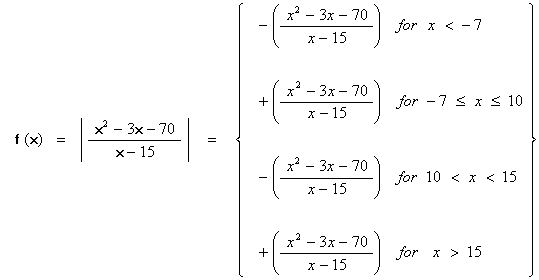
HW #6, Part II Problems:

   In each problem, for the given function f(x), determine a piece-wise defined formula for f(x) which does not involve the absolute value function:

Problems  1 – 4 :

    |