Saturday Morning Math Group

Spring 2004 Presentations

 

Spring 2004 Talks!
  • February 7, 2004
    • Location:RLM 4.102 (On the UT campus)
    Group Leader: Dr. Oscar Gonzalez -------------->
    Topic: Optimization, i.e., how to do things the easy way!
    Title: "Queen Dido's Problem"
    Poster: To view the poster advertising this SMMG, click here.

    Queen Dido's Problem came from a story described in Virgil's Aneid. Queen Dido is on the run from her evil brother, and flees to North Africa.

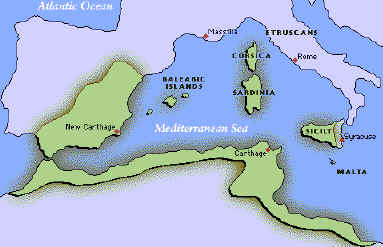
    She arrives at what becomes known as Carthage (nowadays Tunisia). Queen Dido wants to buy some land from the local ruler, King Jambas, so they agree that she can buy all the land that she could enclose with a bull's hide. Queen Dido has the bull's hide cut into small strips and stitches the strips together.

    Now, Queen Dido wants as much land as possible, right? And, since she knows her geometry, she outlines the shape with the biggest area possible. What shape does she outline with the bull's hide? The city is on the sea, so she even uses a further trick...can you think what that would be?

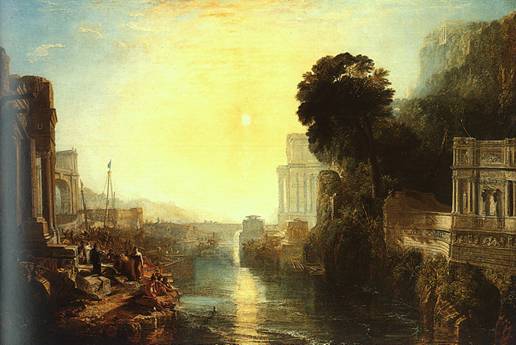
    This is a painting by Joesph Mallord William Turner, 1775-1851. It is of the city of Carthage
    See you at SMMG!

    Pictures are in! Click HERE to check them out.

    Click here to download a copy of the handout from this SMMG.

  • March 6, 2004
    • Location:RLM 4.102 (On the UT campus). From 10:00 AM - 12:30 PM
    Group Leader: Dr. Chaim Goodman-Strauss -------------->
    Topic:Topology/Geometry
    Title:The Shape of Symmetry
    Poster:To download or view a copy of the poster advertising this SMMG, click here.

    Symmetrical patterns surround us--- on our clothes, our floors, our architecture, even our gift-wrap! For over 20,000 years people have been inventing such decorative patterns, but mathematicians began to understand them well just within the last century. The correct mathematical perspective is less than twenty years old, and surprisingly, comes from the branch of mathematics known as Topology ("rubber sheet geometry").
    Check out some of the symmetries in these pictures:

    Pictures are in! Click here to see the pictures from Saturday, March 6th.

  • March 27, 2004
    • Group Leader: Dr. Dan Bonevac -------------->
    Location:RLM 4.102 (On the UT campus)
    Topic: Mathematics and Philosophy, What's the Paradox?
    Title: "Gödel's Theorems!"
    Poster: To view the poster advertising this SMMG, click here.

    Perhaps the greatest logician of all times, he [Kurt Gödel] brought a revolution to mathematical thought with his Incompleteness Theorem which states, in simple terms, that our axioms for the natural numbers do not guarantee that all conceivable statements are decidable (true or false). More astonishingly, it is impossible to create such a "complete" axiomatic system. There will always remain statements that are neither true nor false i.e impossible to be proved or refuted.

    Godel's Incompleteness Theorem states that in any consistent formal system which is adequate for arithmetic there is a true but unprovable sentence. What did this mean for mathematics? Well as Gregory Chaitin put it:

    "At the time of its discovery, Kurt Gödel's incompleteness theorem was a great shock and caused much uncertainty and depression among mathematicians sensitive to foundational issues, since it seemed to pull the rug out from under mathematical certainty, objectivity, and rigor." - Gregory J. Chaitin

    Russell's Paradox is an example of an incomplete system. A description of it can be found at the "Russell's Paradox" web site http://users.forthnet.gr/ath/kimon/Russells_pdx.html.

    Pictures are in!Click here to see pictures from the March 27th SMMG!
    To download a copy of the handout that was used during this SMMG, click here.

  • April 24, 2004
    • Group Leader: Dr. David J. Saltman -------------->
    Location:RLM 4.102 (On the UT campus)
    Topic: Cryptology
    Title: "Fighting WWII with Permutations"
    Poster: To view the poster advertising this SMMG, click here.


    During World War II, the German Air Force, Army, and Navy all used similar code machines that the Allies called ``Enigma''. Battles were won, and convoys saved, partly because the Allies could read much of the German radio messages to airplanes, submarines, and armies fighting in the war. The first achievements were due to a very small group of Polish mathematicians, and after the defeat of Poland their successes were magnified and improved by a huge effort of British mathematicians, engineers, and code breakers including Alan Turing. The underlying mathematics of Enigma is itself fascinating, relying on studying permutations and other basic mathematical objects. We will talk about codes and ciphers in general, and specifically about the Enigma machine. We will try our hand at ``breaking'' easy codes, and get some idea how to break very hard codes like Enigma. We will even talk a bit about how this mathematics was so very important in the war.

    The Enigma!
    Click http://www.mtholyoke.edu/~adurfee/cryptology/enigma_j.html to go to a website that has an Applet of an Enigma machine.
    Or try this one, it has a great explanation of the Enigma machine:http://www.ugrad.cs.jhu.edu/~russell/classes/enigma/
    Pictures are in! Click here to check them out.