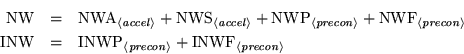Next: Stopping Tests
Up: NSPCG User's Guide
Previous: Storage Modes
Workspace Requirements
In this section, estimated maximum requirements in NSPCG for real
and integer workspace are given. These values should be used initially
for the NW and INW parameters in the NSPCG calling sequence, and
parameters WKSP and IWKSP should be dimensioned to at least NW and
INW, respectively. If insufficient real or integer workspace is
provided, a fatal error occurs with IER set to -2 or -3 and NW or
INW set to the amount of workspace needed at the point execution
terminated. Thus, an easy way to determine storage requirements is
to run the package repeatedly using the values of NW and INW suggested
by NSPCG from the previous run until enough workspace is supplied.
On the other hand, if sufficient real and integer workspace
is provided, NW and INW are set on output to the amount of real and
integer workspace actually required. Thus, workspace requirements can
be reduced to these levels when rerunning the same problem.
Workspace requirements can often be reduced if the user chooses
certain IPARM quantities carefully. For the symmetric accelerators,
the choice of stopping test, as determined by NTEST [= IPARM(1)],
has no effect on workspace requirements. For the nonsymmetric
accelerators, some stopping tests can increase storage demands by
up to 3N. Thus a stopping test should be chosen which is efficient
in time and memory. See Section 10 for information regarding
the selection of stopping tests in the nonsymmetric case.
Also,
2N integer workspace can be saved if the user informs NSPCG whether
or not matrix A has Property A if this property affects a
preconditioner. This is done by setting IPROPA [= IPARM(18)]
appropriately.
In the following formulas, let
| N |
be the problem size |
| MAXNZ |
be the active column width of the COEF array |
| ITMAX |
be IPARM(2) |
| NS1 |
be IPARM(9) |
| NS2 |
be IPARM(10) |
| LVFILL |
be IPARM(16) |
| LTRUNC |
be IPARM(17) |
| IPROPA |
be IPARM(18) |
| KBLSZ |
be IPARM(19) |
| NBL2D |
be IPARM(20) |
| ISYMM |
be IPARM(23) |
| NV |
be
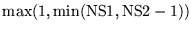 |
| NH |
be
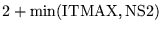 |
| NBLK |
be N/NBL2D |
| NFACTI |
be the number of diagonals in the factorization |
| NCMAX |
be the maximum number of nodes of the same color in a |
| |
multicolor preconditioner |
| KEYGS |
be the gather/scatter switch set in routine DFAULT |
| |
(see Section 18 for details on this switch) |
| DB |
be the full bandwidth of 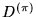 where
where
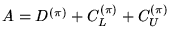 |
| |
in block notation |
| DHB |
be the half bandwidth of 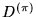 |
| ABAND |
be the full bandwidth of matrix A, in 2-D blocks |
| |
(e.g., ABAND = 3 for a 3-D 7-point operator on a box) |
Then
As noted above,
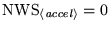 if
if
 accel
accel 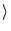 is CG, SI, SOR, SRCG, or SRSI, and can be up to a maximum of
is CG, SI, SOR, SRCG, or SRSI, and can be up to a maximum of
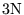 otherwise. A table giving the real workspace required for
each accelerator,
otherwise. A table giving the real workspace required for
each accelerator,
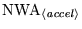 , is given below, followed
by a table giving the real and integer workspace required for each
preconditioner,
, is given below, followed
by a table giving the real and integer workspace required for each
preconditioner,
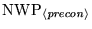 and
and
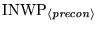 . Finally, a table is shown giving
real and integer workspace requirements for factorizations for certain
preconditioners,
. Finally, a table is shown giving
real and integer workspace requirements for factorizations for certain
preconditioners,
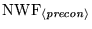 and
and
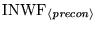 .
.
Table 4:
Values for
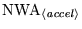
 accel accel  |
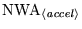 |
| CG |
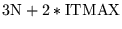 |
| SI |
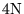 |
| SRCG |
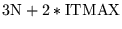 |
| SRSI |
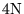 |
| SOR |
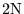 |
| BASIC |
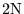 |
| ME |
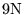 |
| CGNR |
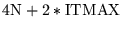 |
| LSQR |
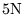 |
| ODIR |
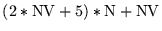 |
| OMIN |
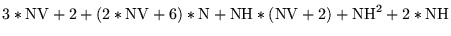 |
| ORES |
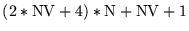 |
| IOM |
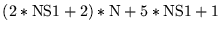 |
| GMRES |
 |
| |
Add
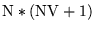 if IQLR =2 or 3
if IQLR =2 or 3 |
| |
Add
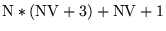 if
if
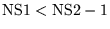 |
| USYMLQ |
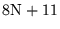 |
| USYMQR |
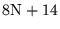 |
| LDIR |
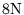 |
| LMIN |
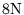 |
| LRES |
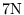 |
| BCGS |
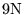 |
| CGCR |
OMIN workspace plus
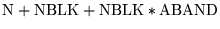 |
|
Table 5:
Values for
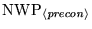 and
and
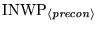
 precon precon  |
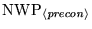 |
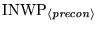 |
| RICH1 |
0, N if KEYGS = 1 |
0 |
| JAC1 |
0, N if KEYGS = 1 |
0 |
| SOR1 |
N |
0 |
| SSOR1 |
N, 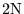 if ISYMM = 1
if ISYMM = 1 |
0 |
| IC1 |
N |
0 |
| MIC1 |
N |
0 |
| LSP1 |
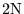 , ,
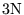 if KEYGS = 1
if KEYGS = 1 |
0 |
| NEU1 |
N, 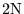 if KEYGS = 1
if KEYGS = 1 |
0 |
| RICH2 |
0 |
0 |
| JAC2 |
0 |
0 |
| LJAC2 |
0 |
0 |
| LJACX2 |
0 |
0 |
| SOR2 |
0 |
MAXNZ |
| SSOR2 |
0 |
MAXNZ |
| IC2 |
0 |
NFACTI |
| MIC2 |
0 |
NFACTI |
| LSP2 |
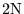 |
0 |
| NEU2 |
N |
0 |
|
Table 6:
Values for
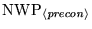 and
and
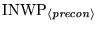 ,
cont.
,
cont.
 precon precon 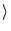 |
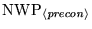 |
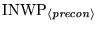 |
| LSOR2 |
0 |
0 |
| LSSOR2 |
N |
0 |
| BIC2 |
KBLSZ |
0 |
| MBIC2 |
KBLSZ |
0 |
| BICX2 |
KBLSZ |
0 |
| MBICX2 |
KBLSZ |
0 |
| LLSP2 |
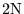 |
0 |
| LNEU2 |
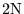 |
0 |
| RICH3 |
0 |
0 |
| JAC3 |
0 |
0 |
| LJAC3 |
0 |
0 |
| LJACX3 |
0 |
0 |
| SOR3 |
0 |
MAXNZ |
| SSOR3 |
N |
MAXNZ |
| IC3 |
0 |
NFACTI |
| MIC3 |
0 |
NFACTI |
| LSP3 |
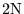 |
0 |
| NEU3 |
N |
0 |
| LSOR3 |
0 |
0 |
| LSSOR3 |
N |
0 |
| BIC3 |
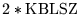 |
0 |
| MBIC3 |
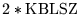 |
0 |
| BICX3 |
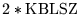 |
0 |
| MBICX3 |
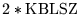 |
0 |
| LLSP3 |
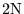 |
0 |
| LNEU3 |
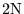 |
0 |
| RICH4 |
0, 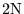 if KEYGS = 1
if KEYGS = 1 |
0 |
| JAC4 |
0, 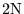 if KEYGS = 1
if KEYGS = 1 |
0 |
| LSP4 |
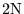 , ,
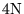 if KEYGS = 1
if KEYGS = 1 |
0 |
| NEU4 |
N, 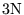 if KEYGS = 1
if KEYGS = 1 |
0 |
| RICH5 |
0, 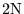 if KEYGS = 1
if KEYGS = 1 |
0 |
| JAC5 |
0, 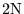 if KEYGS = 1
if KEYGS = 1 |
0 |
| LSP5 |
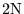 , ,
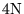 if KEYGS = 1
if KEYGS = 1 |
0 |
| NEU5 |
N, 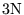 if KEYGS = 1
if KEYGS = 1 |
0 |
| SOR6 |
N |
0 |
| SSOR6 |
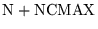 |
0 |
| IC6 |
N |
0 |
| MIC6 |
N |
0 |
| RS6 |
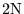 |
0 |
| SOR7 |
0 |
0 |
| SSOR7 |
N |
0 |
| BIC7 |
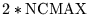 |
0 |
| MBIC7 |
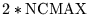 |
0 |
| BICX7 |
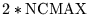 |
0 |
| MBICX7 |
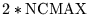 |
0 |
| RS7 |
N |
0 |
|
Table 7:
Values for
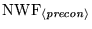 and
and
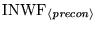
 precon precon  |
Case |
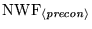 |
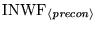 |
| IC1, |
IPROPA = 1, LVFILL = 0 |
N |
0 |
| MIC1 |
IPROPA = 0, LVFILL = 0, ISYMM = 0 |
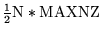 |
0 |
| |
IPROPA = 0, LVFILL = 0, ISYMM = 1 |
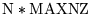 |
0 |
| |
LVFILL > 0, ISYMM = 0 |
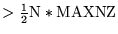 |
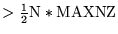 |
| |
LVFILL > 0, ISYMM = 1 |
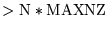 |
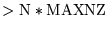 |
| |
IPROPA = 2 |
0 |
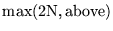 |
| LJAC2 |
all cases |
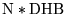 |
0 |
| LJACX2 |
all cases |
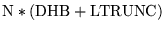 |
0 |
| IC2, |
IPROPA = 1, LVFILL = 0 |
N |
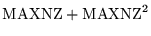 |
| MIC2 |
IPROPA = 0, LVFILL = 0 |
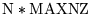 |
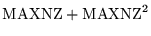 |
| |
LVFILL > 0 |
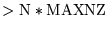 |
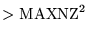 |
| |
IPROPA = 2 |
0 |
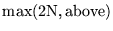 |
| LSOR2 |
all cases |
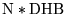 |
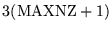 |
| LSSOR2 |
all cases |
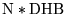 |
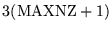 |
| BIC2, |
IPROPA = 1, LVFILL = 0 |
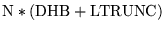 |
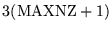 |
| MBIC2, |
IPROPA = 0, LVFILL = 0, LTRUNC = 0 |
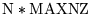 |
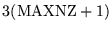 |
| BICX2, |
otherwise |
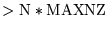 |
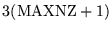 |
| MBICX2 |
IPROPA = 2 |
0 |
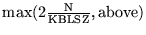 |
| LLSP2 |
all cases |
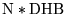 |
0 |
| LNEU2 |
all cases |
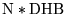 |
0 |
| LJAC3 |
all cases |
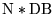 |
0 |
| LJACX3 |
all cases |
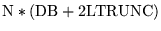 |
0 |
| IC3, |
IPROPA = 1, LVFILL = 0 |
N |
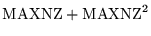 |
| MIC3 |
IPROPA = 0, LVFILL = 0 |
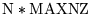 |
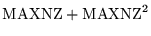 |
| |
LVFILL > 0 |
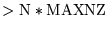 |
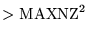 |
| |
IPROPA = 2 |
0 |
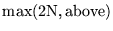 |
| LSOR3 |
all cases |
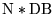 |
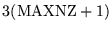 |
| LSSOR3 |
all cases |
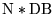 |
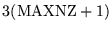 |
| BIC3, |
IPROPA = 1, LVFILL = 0 |
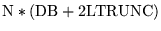 |
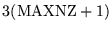 |
| MBIC3, |
IPROPA = 0, LVFILL = 0, LTRUNC = 0 |
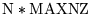 |
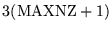 |
| BICX3, |
otherwise |
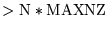 |
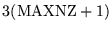 |
| MBICX3 |
IPROPA = 2 |
0 |
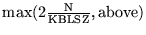 |
| LLSP3 |
all cases |
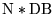 |
0 |
| LNEU3 |
all cases |
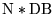 |
0 |
| IC6, |
IPROPA = 1, LVFILL = 0 |
N |
0 |
| MIC6 |
IPROPA = 0, LVFILL = 0 |
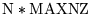 |
0 |
| |
LVFILL > 0 not allowed |
|
|
| |
IPROPA = 2 |
0 |
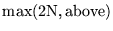 |
| SOR7 |
all cases |
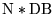 |
|
| SSOR7 |
all cases |
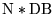 |
|
| BIC7, |
IPROPA = 1 |
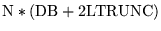 |
|
| MBIC7, |
IPROPA = 0, LTRUNC = 0 |
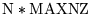 |
|
| BICX7, |
else |
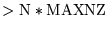 |
|
| MBICX7 |
|
|
|
| RS7 |
all cases |
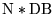 |
|
| others |
all cases |
0 |
0 |
|




Next: Stopping Tests
Up: NSPCG User's Guide
Previous: Storage Modes