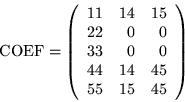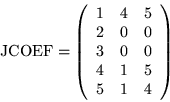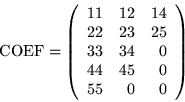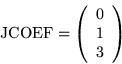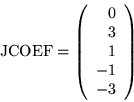Storage Modes

Many factors must be taken into account when choosing the operator representation for A in an iterative solution method. An iterative solver is typically one of many components in an application, and the application may suggest an appropriate iterative solution method and representation of the operator. For example, in many finite element applications, it is convenient to represent the global stiffness matrix A in an element-based data structure rather than assembling it explicitly. A suitable iterative method in that case might be an acceleration without preconditioning since it is then only necessary to compute matrix-vector products which can be computed using the element stiffness matrices in an element-by-element approach. Also, resource limitations of the computer may affect the method of representing the operator A. Storage demands may require that the matrix be regenerated for every iteration or that the effect of an application of the operator A on a vector be represented implicitly. For details in using NSPCG in matrix format-free mode, see Section 17.

The properties of the operator may also have a strong bearing on the choice of operator representation. The most efficient iterative solution codes exploit knowledge of any special characteristics of the matrix such as nonzero pattern, symmetry in structure or coefficients, and the presence or absence of constant coefficients. For purposes of computational and storage efficiency, a sparse matrix data structure should normally be chosen which matches the sparsity pattern of the operator A. In particular, the vectorization and parallelization of preconditioners depends strongly upon the exploitation of the sparsity pattern. If, on the other hand, a sparse matrix data structure is not compatible with the matrix sparsity pattern, the potential of storing and doing computations with too many zeros arises. Symmetry in matrix structure or coefficients may allow economies in storage costs. Finally, if the operator has constant coefficients, it would be wasteful in a production code to use a data structure which stores all the nonzero coefficients of the matrix.

NSPCG currently allows several storage modes for representing the coefficient matrix. A short description of each follows. In considering these storage schemes, the user should select the scheme most convenient for the application. If the matrix has a diagonal or block structure, then storage by diagonals can be a very efficient way to represent the matrix. Also, block preconditioners can be selected with this storage mode, many of which have excellent convergence properties. In addition, many computations vectorize with this storage mode, making the package more efficient on pipelined computers. On the other hand, if the matrix is unstructured, then storage by diagonals will result in a great many zeros being stored and computed upon. In this case, the primary storage format may be more desirable. The primary format will be efficient if there is a relatively constant number of nonzeros per equation. If one equation has many more nonzeros than the rest, then MAXNZ will have to be large enough to accommodate it, resulting in many zeros being stored for the other equations. If this is the case, coordinate storage format can be used.

Primary Format

: In this storage format, there are two rectangular arrays COEF and JCOEF, one real and one integer, which are used to store a representation of the coefficient matrix. Both arrays are dimensioned NDIM by MDIM, where NDIM is at least as large as N, the size of the system, and MDIM is at least as large as MAXNZ, the maximum number of nonzeros per row in the matrix, with the maximum being taken over all rows. Each row in COEF will contain the nonzeros of the corresponding row in the full matrix A, and the corresponding row in JCOEF will contain its respective column numbers. 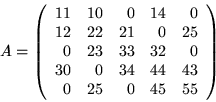For example, the matrix

$$A = \left(\begin{array}{rrrrr} 11 & 0 & 0 & 14 & 15 \\ 0 &... ... & 0 & 44 & 45 \\ 15 & 0 & 0 & 45 & 55 \end{array} \right)$$

would be represented in the COEF and JCOEF arrays as

$$\mbox{COEF} = \left(\begin{array}{rrr} 11 & 14 & 15 \\ 22 ... ... & 0 \\ 44 & 14 & 45 \\ 55 & 15 & 45 \end{array} \right)$$

$$\mbox{JCOEF} = \left(\begin{array}{rrr} 1 & 4 & 5 \\ 2 & 0... ... 3 & 0 & 0 \\ 4 & 1 & 5 \\ 5 & 1 & 4 \end{array} \right)$$

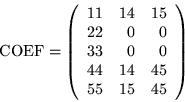
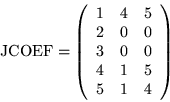
There are several remarks which should be made --

1.

If a row in matrix A has fewer than MAXNZ nonzeros, the corresponding rows in COEF and JCOEF should be padded with zeros.

2.

The nonzero entries in a given row of COEF may appear in any order. However, if the diagonal element is not in column one, then NSPCG will place it there without returning it to its original position on exiting.

3.

Several splittings will attempt to rearrange COEF and JCOEF in order to make the preconditioning solution process more efficient and vectorizable. They may even attempt to expand the matrix within the limit set by MDIM, increasing MAXNZ in the process. However, the matrix returned in COEF and JCOEF at output will be equivalent to the one at input to within roundoff error. Slight roundoff error in the coefficient arrays and RHS will result if the user requests that scaling of the matrix be done.

4.

For this data format, all nonzero matrix entries must be present even if the matrix is symmetric. It does not suffice to store just the upper or lower triangle of the matrix A.

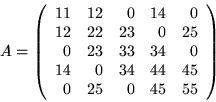
Symmetric Diagonal Format

: This storage format uses a real rectangular array and an integer vector to store a representation of the matrix. COEF is dimensioned NDIM by MDIM and JCOEF is dimensioned to length MDIM. NDIM is at least as large as N, the size of the linear system, and similarly MDIM is at least as large as MAXNZ, the number of diagonals to be stored. Each column of COEF contains a diagonal of A and JCOEF contains a nonnegative integer for each diagonal indicating its distance from the main diagonal. For example, the main diagonal has a distance of 0, the first superdiagonal has a distance of 1, etc. This storage format may be used only if matrix A is symmetric. Only the main diagonal and nonzero diagonals appearing in the upper triangular part of A are stored. For example, the matrix

$$A = \left(\begin{array}{rrrrr} 11 & 12 & 0 & 14 & 0 \\ 12 ... ...& 34 & 44 & 45 \\ 0 & 25 & 0 & 45 & 55 \end{array} \right)$$

would be represented in the COEF and JCOEF arrays as

$$\mbox{COEF} = \left(\begin{array}{rrr} 11 & 12 & 14 \\ 22 ... ... 34 & 0 \\ 44 & 45 & 0 \\ 55 & 0 & 0 \end{array} \right)$$

$$\mbox{JCOEF} = \left(\begin{array}{r} 0 \\ 1 \\ 3 \end{array} \right)$$

There are several remarks which should be made --

1.

Element a_ij of the matrix always appears in row i of the COEF array. Short diagonals must be padded with zeros at the bottom. In other words, the diagonals are top-justified.

2.

The diagonals of A may be stored in any order. However, if the main diagonal of A does not appear in column one of COEF, then NSPCG will place it there without returning it to its original position on exiting.

3.

As with the previous format, many preconditioners will attempt to rearrange COEF and JCOEF and possibly expand COEF within the limit set by MDIM, changing MAXNZ in the process.

Nonsymmetric Diagonal Format

: This storage format is similar to the one described above except that all nonzero diagonals must be stored. If a diagonal of A is below the main diagonal, it's corresponding entry in JCOEF is negative. Thus, the first sub-diagonal has a JCOEF entry of -1, the second sub-diagonal has a JCOEF entry of -2, etc. This storage format is intended for nonsymmetric diagonally structured matrices. For example, the matrix

$$A = \left(\begin{array}{rrrrr} 11 & 10 & 0 & 14 & 0 \\ 12 ... ...& 34 & 44 & 43 \\ 0 & 25 & 0 & 45 & 55 \end{array} \right)$$

would be represented in the COEF and JCOEF arrays as

$$\mbox{COEF} = \left(\begin{array}{rrrrr} 11 & 14 & 10 & 0 & ... ...& 43 & 34 & 30 \\ 55 & 0 & 0 & 45 & 25 \end{array} \right)$$

$$\mbox{JCOEF} = \left(\begin{array}{r} 0 \\ 3 \\ 1 \\ -1 \\ -3 \end{array} \right)$$

There are several remarks which should be made --

1.

Element a_ij of the matrix always appears in row i of the COEF array. Short diagonals should be padded at the bottom with zeros if they are superdiagonals and should be padded at the top with zeros if they are subdiagonals. Thus, superdiagonals are top-justified and subdiagonals are bottom-justified.

2.

The diagonals of A may be stored in COEF in any order. However, if the main diagonal of A does not appear in column one of COEF, then NSPCG will place it there without returning it to its original position on exiting.

3.

As with the previous format, many preconditioners may attempt to rearrange COEF and JCOEF and possibly expand COEF within the limit set by MDIM, changing MAXNZ in the process.

Symmetric Coordinate Format

: This storage format uses a real vector and an integer array to store a representation of the matrix. COEF is dimensioned to length NDIM and JCOEF is dimensioned NDIM by 2. COEF contains the nonzero elements of the matrix and JCOEF contains the corresponding i values in column 1 and the corresponding j values in column 2. Thus if COEF(k) = a_i,j, then JCOEF(k,1) =i and JCOEF(k,2) =j. NDIM is at least as large as MAXNZ, the number of nonzeros stored, and MDIM can be set to anything. This storage format may be used only if matrix A is symmetric. Only the main diagonal and nonzero coefficients appearing in the upper triangular part of A are stored. For example, the matrix

$$A = \left(\begin{array}{rrrrr} 11 & 12 & 0 & 14 & 0 \\ 12 ... ...& 34 & 44 & 45 \\ 0 & 25 & 0 & 45 & 55 \end{array} \right)$$

would be represented in the COEF and JCOEF arrays as

$$\mbox{COEF} = (11,22,33,44,55,12,23,34,45,14,25)$$

$$\mbox{JCOEF} = \left(\begin{array}{cc} 1 & 1 \\ 2 & 2 \\ ... ... 3 & 4 \\ 4 & 5 \\ 1 & 4 \\ 2 & 5 \end{array} \right)$$

For this example, N =5, MAXNZ =11, NDIM =11, and MDIM can be set to anything. There are several remarks which should be made --

1.

All elements of the main diagonal must be stored, even if some are zeros.

2.

Duplicate entries (entries having the same i and j coordinates) are allowed. NSPCG removes duplicates by adding their corresponding coefficient values. Thus, MAXNZ may be reduced upon output.

3.

The nonzeros of A may be stored in any order. However, NSPCG will rearrange the elements of the COEF and JCOEF arrays into a convenient order without returning it to its original position on exiting. In particular, the diagonal elements of the matrix will be placed into the first N locations of COEF.

Nonsymmetric Coordinate Format

: This storage format is similar to the one described above except that all nonzero coefficients must be stored. This storage format is intended for nonsymmetric matrices. For example, the matrix

$$A = \left(\begin{array}{rrrrr} 11 & 10 & 0 & 14 & 0 \\ 12 ... ...& 34 & 44 & 43 \\ 0 & 25 & 0 & 45 & 55 \end{array} \right)$$

would be represented in the COEF and JCOEF arrays as

$$\mbox{COEF} = (11,22,33,44,55,14,25,10,21, \\ 32,43,12,23,34,45,30,25)$$

$$\mbox{JCOEF} = \left(\begin{array}{cc} 1 & 1 \\ 2 & 2 \\ ... ... 4 & 3 \\ 5 & 4 \\ 4 & 1 \\ 5 & 2 \end{array} \right)$$

For this example, N =5, MAXNZ =17, NDIM =17, and MDIM can be set to anything. The remarks regarding symmetric coordinate storage format apply for the nonsymmetric format also.