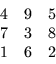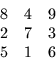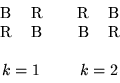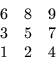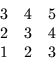Next: Error Conditions
Up: NSPCG User's Guide
Previous: Using Reduced System Methods
Using Multicolor Orderings
For many iterative methods, the unknowns are updated in an order
other than the natural (or lexicographical) ordering. The order
in which the unknowns are updated can be specified by imposing a
coloring on the mesh so that all the unknowns corresponding to nodes
of a particular color are updated before the unknowns corresponding
to nodes having a different color. Typically, a coloring is chosen
so that unknowns (nodes) of the same color are decoupled, thus
allowing these unknowns to be updated simultaneously. This
property makes multicolor iterative methods especially attractive
on vector or parallel computers.
NSPCG allows the matrix A to be reordered and permuted
according to a coloring. The user can request that the matrix A
be permuted before iterating by filling vector P in the NSPCG calling
sequence with a coloring vector and setting IPERM [= IPARM(14)] to
one. A coloring is defined as the assignment to each equation of
an integer signifying the number of the color. If the mesh is to be
colored with p colors, vector P contains for each equation
an integer between 1 and p, inclusive. NSPCG will number those
equations labeled with 1 first, followed by those equations labeled
with 2, and so on. Equations labeled with p will be numbered
last. NSPCG then permutes the matrix according to the new ordering
of the equations before the iteration begins. After iteration has
terminated, the matrix is permuted to its original form.
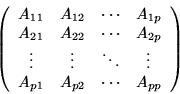
If a matrix whose mesh is colored with p colors is permuted
according to the colors, the resulting matrix can be viewed as a
p by p block matrix:
There are some restrictions on the use of permutations:
- If a permutation is requested with the primary storage
format, the allowable preconditioners are SOR6, SSOR6,
IC6, MIC6, and RS6. In this case, the coloring vector P
must be chosen so that the diagonal block submatrices
Aii are diagonal. Thus, equations having the same
color cannot be dependent. This requirement is made so
that vectorization of these methods is possible. Otherwise,
complicated block solves would be necessary for each
diagonal block instead of a simple vector operation,
and the primary storage format is not informative enough
to vectorize such operations.
- If a permutation is requested with a diagonal storage
format, the allowable preconditioners are SOR7, SSOR7,
BIC7, BICX7, MBIC7, MBICX7, and RS7. In this case,
the coloring vector P can be chosen so that the Aii
submatrices are banded. If they are banded, their
bands must be dense.
- If a permutation is requested with a diagonal storage
format, extra diagonals are often created. NSPCG will
abort unless the column dimensions of the COEF and JCOEF
arrays are set large enough to store the permuted matrix
by diagonals.
- If a permutation is requested with a coordinate storage
format, the allowable preconditioners are RICH5, JAC5,
NEU5, and LSP5. There are no restrictions for permutations
used with coordinate storage format, but permutations
are not effective with these preconditioners.
When using the NSPCG package, the differences between ``block" and
``multicolor" methods are as follows:
- 1.
- The name of a block preconditioner must end with a 2 or
a 3, while the name of a multicolor preconditioner must
end with a 6 or a 7.
- 2.
- A multicolor preconditioner can only be applied after a
permutation of the matrix (i.e., vector P must be set to a
coloring vector and IPERM [= IPARM(14)] must be set to one).
A block preconditioner can only be applied to a matrix
which is not permuted by NSPCG.
- 3.
- With a block method, the diagonal block matrices
Aii must be of equal size, which the user must
specify with KBLSZ [= IPARM(19)]. With a multicolor
method, the Aii are not required to be of equal
size.
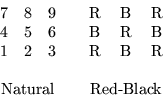
As an example of a coloring, suppose the user requests that a 3
by 3 mesh with the natural ordering be given a red-black ordering:
If the red unknowns are to be labeled first, then P would be
chosen as
P = ( 1, 2, 1, 2, 1, 2, 1, 2, 1)
resulting in the ordering:
If the user wished the black unknowns to be labeled first, P would
be chosen as
P = ( 2, 1, 2, 1, 2, 1, 2, 1, 2)
resulting in the ordering:
If a preconditioner requires a permutation then the user must set
IPERM [= IPARM(14)] equal to one and fill P with a coloring vector.
There are two facilities in NSPCG for automatically generating coloring
vectors -- REDBLK and COLOR.
- 1.
- REDBLK determines whether or not matrix A has Property A.
If it does, REDBLK generates a coloring vector for point
red-black ordering. The calling sequence for REDBLK is
CALL REDBLK (NDIM,N,MAXNZ,COEF,JCOEF,P,IP,NSTORE,IWKSP,IER)
The parameters NDIM, MAXNZ, COEF, JCOEF, N, and NSTORE
have been explained previously. P, IP, and IWKSP are integer
workspace vectors of length N on input. On output, P
contains the coloring vector if IER =0. If IER =-8,
the matrix does not have Property A, and a red-black
coloring vector does not exist and the user must choose
some other iterative method.
- 2.
- COLOR replicates a rectangular (2-D) or box (3-D) color
pattern throughout a rectangular or box domain. For
example, a red-black pattern on a 2-D rectangular grid
is a replication of the pattern:
The calling sequence for COLOR is
CALL COLOR (NXP,NYP,NZP,NX,NY,NZ,PATT,P)
NXP, NYP, and NZP are the x,y, and z dimensions of the
pattern, and NX, NY, and NZ are the dimensions of the grid.
For 2-D problems, NZP and NZ are both set to 1. PATT is an
integer vector of length NXP*NYP*NZP containing the pattern
in the order left-to-right, bottom-to-top. Different colors
are coded as different integers in PATT, starting with one.
P is an integer vector of length NX*NY*NZ which contains
the coloring vector on output. For example, the color
pattern
would be specified with NXP =2, NYP =2, NZP =1, and
PATT
=(1,2,2,1). A red-black pattern in three dimensions
whose pattern is given by
would be specified with NXP =2, NYP =2, NZP =2, and
PATT
=(1,2,2,1,2,1,1,2). A line red-black pattern in two
dimensions with the lines of the same color running
horizontally as in the pattern
would be specified with NXP =1, NYP =2, NZP =1, and
PATT =(1,2). The 4-color pattern in two dimensions
would be specified with NXP =2, NYP =2, NZP =1, and
PATT
=(1,2,3,4). A 4-color pattern is often applied
to matrices resulting from a 9-point finite difference stencil.
There are many interesting colorings which cannot be generated
by either REDBLK or COLOR since they do not represent replications
of a rectangular pattern. One such coloring is ordering by
diagonals along a rectangular mesh:
Such orderings are useful when the stencil is a 5-point star,
because they allow vectorization along diagonals for such methods
as SOR and IC(0). The coloring vector for such an ordering is
or
P = (1,2,3,2,3,4,3,4,5)




Next: Error Conditions
Up: NSPCG User's Guide
Previous: Using Reduced System Methods