This set of problems focuses on the residue theorem, argument principle, and existence of branches. Some more problems on topics from the last post are also included.

Resources

Ahlfors section 4.4-4.6

Problems

Problem 1 (Prelim August 2015)

Let $f$ be a non-constant meromorphic function satisfying \(f(z) = f(z+\sqrt{2}) = f(z+i\sqrt{2})\) and assume $f$ has at most a single pole in $\mathbb{D} = \{z: |z| < 1 \}$.

1. Show that there must exist a pole in $\mathbb{D}$.
   Hint

   If there is no pole in $\mathbb{D}$ how many poles can $f$ have elsewhere?
   Solution

   Note that we can fit a square in side of $\mathbb{D}$ with sides parallel to the real/imaginary axes and with lengths $\sqrt{2}$. If there is no pole in this square then $f$ is bounded on it. However, since our periods are $\sqrt{2},i\sqrt{2}$ it would then follow that $f$ is bounded on all of $\mathbb{C}$ - hence its entire and by Liouville's theorem must be constant. Therefore, there exists at least one pole in this square contained in $\mathbb{D}$.
2. Show that this pole cannot be simple.
   Hint

   Try integrating along a square with side lengths $\sqrt{2}$.
   Solution

   We can parameterize a path along the square from part (a) by $\gamma:[0,1] \to \mathbb{C}$ a piecewise linear function $\gamma$
   
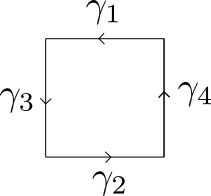
   Note that due to the period, the values of $f$ along $\gamma_1$ and $\gamma_2$ are identical, however we are now traversing in the opposite direction so $\gamma_1' = -\gamma_2'$. This gives us the relationship $$ \begin{align*} \int_{\gamma_2} f\,dz &= \int_{0}^{1/4} \gamma'_2(t+1/2) f(\gamma_2(t+1/2))\,dt \\&= -\int_{1/4}^0 \gamma_2'(3/4-u) f(\gamma_2(3/4 - u))\,du \\&= -\int_0^{1/4} \gamma_1'(u)f(\gamma_1(u))\,du = - \int_{\gamma_1} f\,dz\end{align*}$$ The same applies to $\gamma_3$ and $\gamma_4$. Hence, if our pole lies at $z_0 \in \mathbb{D}$, we find $$ 2\pi i\text{res}(f,z_0) = \int_\gamma f\,dz = 0 $$ allowing us to conclude that the pole at $z_0$ is not simple.

Problem 2 (Prelim January 1997)

Suppose that $f$ is a holomorphic function on a neighborhood of $\overline{\mathbb{D}}$ and on $\partial \mathbb{D}$ $f$ satisfies $|f(z)| \leq a$ when $\text{Im}(z) \geq 0$ and $|f(z)| \leq b$ when $\text{Im}(z) \leq 0$. Show that [ |f(0)| \leq \left(ab\right)^{1/2}. ]

Problem 3 (Prelim August 1996)

Suppose $f$ is analytic on an open neighborhood of $\overline{\mathbb{D}}$ and that it is injective on $|z| = 1$. Show that $f$ is injective on $\mathbb{D}$.

Problem 4 (Prelim January 2022)

Let $K$ be a compact connected subset of $\mathbb{C}$ containing $\pm i$. Show that there exists a holomorphic branch of $(z^2 + 1)^{-1/2}$ in $\mathbb{C} \setminus K$ and determine the possible values of its integral along closed curves in $\mathbb{C} \setminus K$.

Solution

Letting $f(z) = (z^2 + 1)^{-1/2}$ we can compute that $$ \frac{f'(z)}{f(z)} = -\frac{z}{z^2 + 1} $$ which has poles of order $2$ at $\pm i$. We then compute $$\text{res}_{z= i}\left( \frac{f'}{f}\right) = \lim_{z\to i} -(z-i) \frac{z}{(z^2 + 1)^2} = -\frac{i}{2i} = -\frac{1}{2} $$ and performing the same computation at $z = -i$ we find $$ \text{res}_{z = -i}\left(\frac{f'}{f}\right) = -\frac{1}{2} = \text{res}_{z = i}\left(\frac{f'}{f}\right) $$ as well. Finally, if $\gamma$ is a closed curve in $\mathbb{C}\setminus K$ the residue theorem gives us that $$ \int_\gamma \frac{f'}{f}\,dz = -i\pi (n(\gamma, i) + n(\gamma, -i)). $$ We now note that $n(\gamma,i) = n(\gamma,-i)$ for any such curve divides $\mathbb{C} \setminus \gamma(I)$ into connected components with identical index. Therefore, $$ \int_\gamma \frac{f'}{f}\,dz = -2i\pi k $$ for $k\in \mathbb{Z}$. In general, we know that a logarithm of a function $f$ exists when this integral is zero for all closed curves $\gamma$ so we are not fortunate enough to arrive at a branch fo $\log(f)$. However, since the integral over closed $\gamma$ is always a multiple of $2\pi i$ we see that it matches the period of $\text{exp}$. As a result, we can define a multivalued map $h:\mathbb{C} \setminus K \to \mathbb{C}$ by fixing some $z_0 \in \mathbb{C}\setminus K$ and letting $l = \log f(z_0)$ for any branch of $\log$ and $\sqrt{}$ with appropriate domains. Then $$ h(\xi) = \left\{ l + \int_{\gamma} \frac{f'}{f}\,dz: \gamma: [0,1], \gamma(0) = z_0, \gamma(1) = \xi \right\}.$$ (Note that this is assuming that there is just one connected component in $\mathbb{C} \setminus K$. This is not necessarily true, but we can define $h$ on other components by fixing other $z_0$ in that component and working piecewise.) From prior work we see the values of $h(\xi)$ all differ by multiples of $2\pi i$ hence $z \mapsto \exp(h(z))$ is a well defined function. We can also see that this function is holomorphic, for if we select any $z$ in the domain there exists a simply connected neighborhood $U$ of $z$ for which $$ \int_\gamma \frac{f'}{f}\,dz = 0$$ for all closed curves $\gamma:[0,1]\to U$. Hence we can locally define a holomorphic branch $l$ of $\log f$ on this domain and in $U$ $\text{exp}(h(z)) = \text{exp}(l(z))$ showing the left hand side is indeed holomorphic at $z$.
Finally, we must show that $\text{exp}(h(z))$ is indeed a branch of $f$. Differentiating $\text{exp}(2h(z))/(f(z))^2$ we find $$ \begin{align*} \frac{d}{dz} \text{exp}(2h(z))(z^2 + 1) &= h'(z)\text{exp}(2h(z))f(z) + 2z \text{exp}(2h(z)) \\ &= 2\text{exp}(2h(z)) \left[ \frac{-z}{z^2 + 1} + \frac{z}{z^2 + 1}\right] = 0 \end{align*} $$ showing that the functions are multiples of one another. Finally, evaluating at $z_0$ we see $\text{exp}(h(z_0)) = \text{exp}(l) = f(z_0)$ hence they are identical.
Original solution to second part
To compute the integral of this branch over a closed curve first note that any such curve $\gamma$ can be replaced by a curve on a circle of radius $> R$ with the same integral (due to Cauchy's theorem.) We can let $R$ be greater the largest modulus attained on $K$. Then note our branch restricted to $\mathbb{C} \setminus \overline{B_r(0)}$ can be continued analytically to $\mathbb{C}\setminus [-i,i]$. Finally, we can construct a dumbbell contour along the segment $[-i,i]$ like so

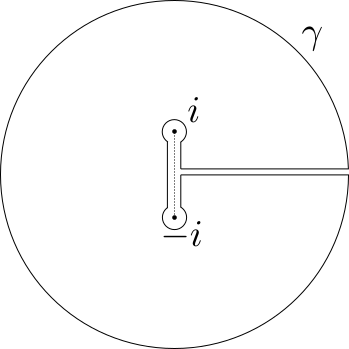
On this contour we first note that as we shrink the dumbbell the contribution from the circular regions goes to zero. Indeed, at $i$ we can let $\gamma(\theta) = re^{i\theta} + i$, then $|(\gamma(\theta)^2 + 1)^{-1/2}| \leq [r(2-r)]^{-1/2}$ after factoring. Then by the ML-lemma we find that $$ \begin{align*} \left| \int_\gamma \sqrt{z^2 + 1} \, dz \right| &\leq L(\gamma)[r(2-r)]^{-1/2} \\ &= 2\pi \frac{\sqrt{r}}{\sqrt{2-r}} \to 0 \end{align*} $$ as $r\to 0$. This shows that integrating along a simple closed circle of radius $> 1$ is equivalent to integrating up and down the segment $[-i,i]$, however when we swap directions we hop over our branch cut so the values will be negated. This negation is justified by the integral of $f'/f$ along any small circle around $\pm i$, which we know gives $\pm \pi i$ so upon exponetiating we will find the across the branch cut our brach differs by a factor of $e^{i\pi}$. Integrating in one direction we find $$ \int_{[-i,i]} \frac{1}{\sqrt{1+z^2}}\,dz = \int_{-1}^1 \frac{i}{\sqrt{1-t^2}}\,dt = \pm \pi i $$ hence the integral over any closed curve will be an integer multiple of $2\pi i$.
Toby's solution to second part
Observe that $$ \left( (1+z^2)^{-1/2} - \frac{1}{z} \right)\left( (1+z^2)^{-1/2} + \frac{1}{z} \right) = \frac{1}{1+z^2} - \frac{1}{z^2} = -\frac{1}{z^2 + z^4} $$ which, for $|z| > 1$, has absolute value below $1/|z|^4$. From this we conclude that one of the products is at most $1/|z|^2$$^\dagger$, this allows us to bound that term by $$ \left| \int_\gamma (1+z^2)^{-1/2} \,dz - \int_\gamma \frac{1}{z} \,dz \right| \leq \int_\gamma \left| \frac{1}{z^2} \right|\,dz \leq \text{Length}(\gamma) \sup |\gamma(t)|^{-2}.$$ Finally, we note that we can homotope $\gamma$ into a sequence of circular loops with arbitrarily large radius $R$, so the right hand side becomes $\leq 2\pi R\cdot R^{-2} \to 0$ as $R\to \infty$, establishing $$ \int_\gamma (1+z^2)^{-1/2} \,dz = \int_\gamma \frac{1}{z} \,dz = 2\pi n$$ for some $n\in \mathbb{Z}$.
$\dagger$ As of writing I'm unsure how to make this step rigorous.

Problem 5 (Prelim August 2020)

Assume $f:\mathbb{C}\setminus \overline{\mathbb{D}} \to \mathbb{D}$ is holomorphic. Prove that $|f’(2)| \leq 1/3$.

Problem 6 (Prelim August 2020)

Suppose that $f$ is analytic on $\mathbb{D}$ and satisfies $|f(z)| \leq M$ for all $z\in \mathbb{D}$. Assume further that $f$ vanishes at the points $ \{z_j\}_{j=1}^N $ where $1 \leq N \leq \infty$.) Prove that

$$ |f(z)| \leq M \left| \prod_{j=1}^m \frac{z-z_j}{1-\overline{z_j}z} \right|\quad \forall z\in\mathbb{D} $$

for any $1 \leq m \leq N$ (or if $N = \infty$ then $1 \leq m < N$. )

Problem 7 (Prelim January 2019)

Given $z\in \mathbb{C}$ and a closed curve in $\mathbb{C}\setminus \{z\}$ denote $n(\gamma,z)$ the index or winding number of $\gamma$ about $z$. If $\gamma$ can be written as [ \gamma(t) = \sum_{k = -N}^{N} c_ke^{ikt} ] with $c_{-N}$ and $c_N$ not both zero show that $-N \leq n(\gamma, z) \leq N$.

Problem 8 (Prelim January 2017)

Prove that the range of the entire function $z\mapsto z^2 + \cos(z)$ is all of $\mathbb{C}$

Problem 9 (Prelim January 2011)

Let $f$ be analytic in an anulus $ U = \{z: r < |z| < R\}$ where $0 < r < R$. Assume $f$ has no zeros in $U$. Show there exists an integer $n$ and a holomorphic function $g:U\to \mathbb{C}$ such that $f(z) = z^n e^{g(z)}$

Problem 10 (Prelim January 2016)

Show that the equation $\sin(f(z)) = z$ has a solution $f$ that is analytic on the region $U = \{z\in \mathbb{C}:|z| < 1\text{ or }\text{Im}(z) \ne 0\}$.

Problem 11 (Prelim August 2016)

Evaluate the integrals [ I = \int_C \sqrt{1-z^2}\,dz \quad J = \int_{0}^\infty \frac{x\sin \pi x}{1-x^2}\,dx ] for some branch of the square root function (indicate which) and $C$ is the positively oriented circle $|z| = 2$.

Solution

For $I$ we can construct a branch of $\sqrt{1-z^2}$ defined on $\mathbb{C}\setminus [-1,1]$ mapping $i \mapsto +\sqrt{2}$. From here, we could proceed identically to problem 4 using a dumbbell contour with "weights" centered at the branch points $z = \pm 1$. In the limiting case as the width of tubes and circles goes to zero we arrive at the integral over $C$ being the same as $$2\int_{-1}^1 \sqrt{1-x^2}\,dx = \pi.$$ To check this, if $\gamma_r$ is a circle of radius $r$ at centered at one of $z = \pm 1$ we find that $$\left| \int_{\gamma_r} \sqrt{1-z^2} \,dz \right| \leq (2\pi r)\sup_{z\in \gamma_r} |\sqrt{1-z^2}| = C2\pi r^{3/2} \to 0$$ as $r \to 0$ by the ML inequality. Next we must justify the resulting integral by looking at our function along the line $0+ir$ as $r\to 0$. Along this branch cut we know that it will approach some value of $\sqrt{1-0^2}$, the branch either being on the positive or negative real axis. We can see that since $i \mapsto +\sqrt{2}$ that the away from the branch cut it is $>0$, but we also know that there are no roots of $1-z^2$ in $i\mathbb{R}$, hence it remains positive for all $r > 0$. This shows that on this side we approach the positive $+\sqrt{1-x^2}$. To see that the other side converges to the negative branch, consider that the residues of $f'/f$ at its poles are $\pi i$, hence sign switches when going around $\pm 1$ (similar to the work done in problem 4.)
Another strategy is to use the substitution $u = z^{-1}$, which transforms integral to be over $|z| = 1/2$ with a single pole inside, allowing us to use the residue theorem. Note that finding the residues can be difficult due to choice of branches.
For $J$ consider the contour that is a large semicircle of radius $R > 0$ with smaller semicircles of radius $r$ cut out at the points $z = \pm 1$.

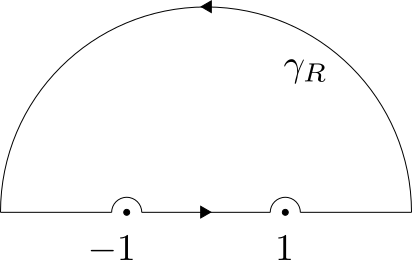
Over this contour we will integrate $$ f(z) = \frac{z e^{\pi i z}}{1-z^2}.$$ First, note that on the largest semicircle we have $$ \begin{align*} \left| \int_{\gamma_R} f(x)\,dx \right| &\leq 2\int_0^{\pi/2} \frac{R^2}{R^2-1} e^{-\pi R\sin \theta}\,d\theta \\&\leq 2\int_0^{\pi/2} \frac{R^2}{R^2-1} e^{-2 R\theta}\,d\theta \\&= \frac{R^2}{R^2 - 1} \left[ \frac{1}{2R} - \frac{1}{2R}e^{-\pi R} \right] \end{align*}$$ which converges to zero as $R \to \infty$. Now, taking the limit as $r\to 0$ of the small circles around the poles at $z = \pm 1$ we see that each circular arc's integral approaches $-\pi i\text{res}_{z = \pm 1}(f)$ (this is because we can write $f(z) = R/(z-p) + g(z)$ where $R$ is the residue at $z = p$ and $g(z)$ is holomorphic near $z = p$. Integrating on the half arc will arrive at $-\pi i R.$ See Ahlfors 4.5.3.) Quick calculations show that $$ \text{res}_{z=1}(f) = \text{res}_{z= -1}(f) = \frac{1}{2} $$ hence by applying Cauchy's theorem and letting $R\to \infty, r\to 0$ we find $$\int_\mathbb{R} f(z)\,dz = \pi i $$ and finally, equating imaginary parts and dividing by 2 (due to evenness of the integrand) we arrive at $$ J = \frac{\pi}{2} $$

Problem 12 (Prelim January 2014)

Suppose $f$ is an entire function with the property that $f(z)$ is real if and only if $z$ is real. Show that $f’(z) \ne 0$ for all real $z$.

Problem 13 (Riccardo’s Quandary)

Consider the following statement: Any function $f$ continuous on the annulus $A = {z\in \mathbb{C}: 1/2 \leq |z| \leq 2}$ such that $f_{\partial A}$ is injective and $f_{A^o}$ is holomorphic is also injective on the interior $A^o$.

1. Find a counter example to this statement.
   Hint

   Try to apply the proof of Problem 3 to this problem, now with a contour of two concentric circles connected by a path. Where does the proof fail in this case?
2. Find an additional hypothesis such that this statement is true. Prove it.
   Hint

   Attempt the simpler case of $f$ having a holomorphic extension in some neighborhood of $A$. To extend this to the case of $A$ just continuous as the boundary prove the *dog on a leash* lemma (if $\gamma,\gamma'$ are two paths in $\C$ such that for all $t$ we have $|\gamma(t) - \gamma'(t)| < |\gamma(t)| then $n(\gamma,0) = n(\gamma',0)$.)

Solution

To begin, we attempt to prove a slightly weaker statement and find where it breaks.
In the case of $f$ extending holomorphically to a neighborhood of $A$ we fix any point $z \in f(A)^o$. Without loss of generality we suppose that $z \not\in [1/2,2].$ We select the contour $\Gamma = \gamma_1 \ast \gamma_2 \ast \gamma_3 \ast \gamma^{-1}_2$ where $\gamma_1$ parametrizes the circle of radius 2 counter clockwise, $\gamma_2$ is a segment connecting $2$ to $1/2$, and $\gamma_3$ is parametrizes the circle of radius 1/2 clockwise.

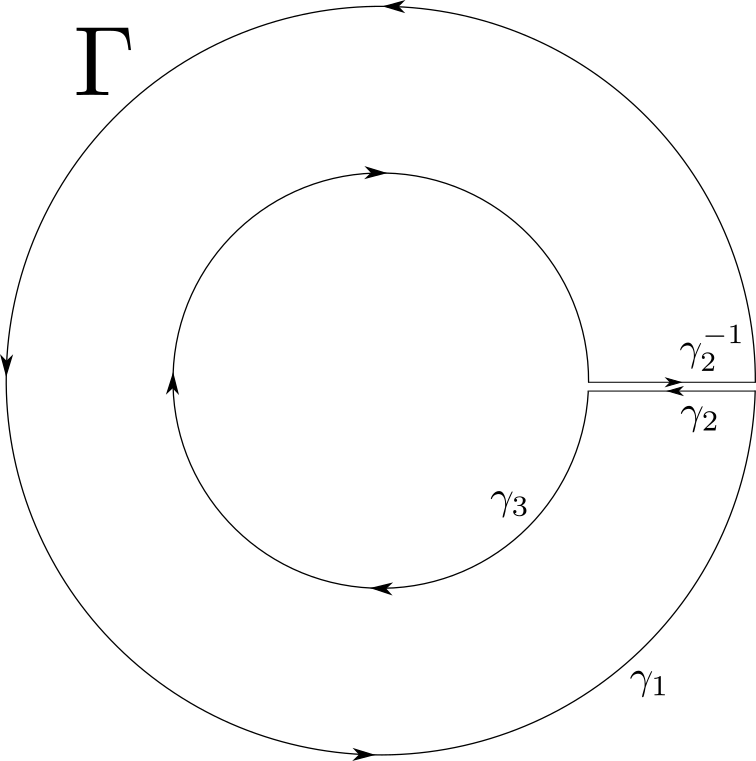
By argument principle we see that the number of solutions $f(\xi) = z$ is exactly $$ \begin{align*} \frac{1}{2\pi i} \int_\Gamma \frac{f'(\xi)}{f(\xi) - f(z)}\,d\xi &= \frac{1}{2\pi i} \left(\int_{f\circ \gamma_1} \frac{1}{\xi - f(z)}\,d\xi + \int_{f\circ \gamma_3} \frac{1}{\xi - f(z)}\,d\xi\right) \\ &= n(f\circ \gamma_1,f(z)) + n(f\circ \gamma_3,f(z)) = \pm 1\text{ or }0. \end{align*}$$ We know that both of these winding numbers are 1, 0, or -1 due to the injectivity of $f$ along $\partial A$, but is it possible for both to be equal to $\pm 1$? The parameterizations of the circles $\gamma_1,\gamma_3$ are oriented in opposite directions so we shall seek an $f$ that reverses the orientation of one and keep the second the same. Such a function is $$ f(z) = z + \frac{2}{z}, $$ because for small $z$ the function resembles $z^{-1}$ which reverses orientation of $\gamma_3$ while for large $z$ it resembles the identity preserving the orientation of $\gamma_1$. From here it is easy to verify $f$ is injective on $\partial A$ and that $f(1) = f(2) = 3$ giving our counterexample for part (a).
This exploration suggests that requiring $f$ to either preserve or reverse orientation for the two circles comprising $\partial A$. For our purposes, we will define this as $n(\gamma_1, z) \ne n(\gamma_3,z)$ for all $z \in \mathbb{C}$. Returning to the attempt at a proof our new assumption guarantees $n(f\circ \gamma_1,f(z)), n(f\circ \gamma_3,f(z))$ cannot both be $1$ or $-1$, hence $n(f\circ \Gamma,z) = \pm 1\text{ or }0$ giving injectivity by the argument principle.
At this point what remains is to extend this result to $f$ analytic in $A^o$ and continuous on $A$. To do this, define $$A_\delta = \{z\in \mathbb{C}: 1/2 + \delta \leq |z| \leq 2 - \delta\}$$ with corresponding contour $\Gamma^\delta$. Due to $A$ being compact $f$ is uniformly continuous on $A$. Given $z\in f(A)^o$ let $\epsilon = d(z, \partial f(A)).$ By uniform continuity there exists $\hat\delta > 0$ such that if $|x-y| < \hat\delta \implies |f(x)-f(y)| < \epsilon$ for all $x,y \in A$. Therefore for any $0 < \delta < \hat\delta$ we have $$ |f\circ \Gamma(t) - f\circ \Gamma^\delta(t)| < \epsilon \leq |f\circ \Gamma(t) - z|.$$ This shows that $\Gamma,\Gamma^\delta$ satisfy the hypothesis of the dog on a leash lemma, hence $$ n(f\circ \Gamma^\delta, z) = n(f\circ \Gamma, z) = \pm 1\text{ or } 0$$ for all sufficiently small $\delta$, and now we are able to apply the argument principle on $\Gamma^\delta$ proving injectivity.