Cooper Faile

Cooper Faile

Math PhD Student at UT Austin

Office: PMA 9.132

Complex Bootcamp Exercises: Products and Series

Published:

This set of problems focuses on series and product representations of holomorphic and meromorphic functions.

Resources

Ahlfors chapter 5.1 - 5.2.3 and 5.3.2

Problems

Problem 1 (Prelim August 2015)

Let $\mu$ be Lebesgue measure on $\mathbb{D}$. Let $H \subset L^2(\mathbb{D},\mu)$ be the subset of holomorphic functions. Show that $H$ is a closed subset.

Hint Show that for every compact subset $K \subset \mathbb{D}$ there exists a constant $C_K > 0$ depending only on $K$ such that $$ \sup_{z\in K} |f(z)| \leq C_k \lVert f|_K \rVert_{L^2}.$$ We can relate the value of $f$ at a point to its integral via the mean value property.
Solution Following the hint, let $K\subset\mathbb{D}$ be compact. Then we can select $r > 0$ such that $d(K,\mathbb{D}\setminus K) > r.$ For $z\in \mathbb{K}$ we can then obtain the following bound by the mean value property $$ |f(z)|^2 \leq \frac{1}{\pi r^2} \int_{B_z(r)} |f(\xi)|^2 \,d\xi $$ which gives us $\sup_{z\in K} |f(z)| \leq C_k \lVert f \rVert_{L^2(\mathbb{D})}$. Note that this is weaker than the statement in the hint, since we are taking the $L^2$ norm over all of the disk rather than just on $K$. Nonetheless, this suffices to show closure of $H$.
Now that we have this bound, take a sequence of functions $\{f_n\}_{n=1}^\infty \subset H$ convering in $L^2$ to $f$. Note that from the bound this sequence is Cauchy sequence with respect to the uniform norm, hence they converge uniformly to a continuous function. By uniqueness of limits in $L^2$, it follows that this continuous limit is equal to $f$ almost everywhere so we can take it to be our representative of $f$. Now, we see $\sup_{z\in K}|f_n(z)-f(z)| \to 0$ on all compact sets, so by Weierstrass' theorem we see that $f$ is holomorphic.

Problem 2 (Prelim January 2022)

Let $0 < \alpha < 1$. Show that [ \prod_{n=1}^\infty \cos(\alpha^n z)] defines an entire function $f$ of finite order. Determine the order and genus of $f$.

Hint It may be difficulty to directly compute the order, but recall that Hadamard's theorem states that if $f$ has genus $h$ and order $\lambda$ then $h \leq \lambda \leq h + 1$.
Solution To see that this product defines an entire function we will show that it converges uniformly on compact sets. Given a compact set $K\subset \mathbb{C}$ we note that it is bounded in modulus by some $M > 0$. Additionally, uniform convergence of the product is the same as uniform convergence of the logarithm of absolute values, so now we consider $$ \begin{align*} \sum_{n=1}^\infty \log|\cos(\alpha^n z)| &= \sum_{n=1}^\infty \log(1 - (1 - |\cos(\alpha^n z)|) ) \\ &\leq \sum_{n=1}^\infty 1 - |\cos(\alpha^n z)| \end{align*} $$ Note that if we expand the $\cos(\alpha^n z)$ terms as Taylor expansion each summand is then $ \alpha^{2n}|z|^2/2 + O(\alpha^{3n} |z|^4)$ showing that this sum can be termwise bounded by $$ C\sum_{n=1}^\infty |\alpha^{n} z |^2 = M^2 \sum_{n=1}^\infty \alpha^n $$ for $n$ sufficiently large. Since $0 < \alpha < 1$ we see that this sum converges, so by the $M$-test the original product converges uniformly on the compact set $K$.
To determine the genus of this product we note that its roots are the set $$ R = \left\{ \left(\frac{\pi}{2} + \pi k\right) \alpha^{-n} : n \in \mathbb{N}, k\in \mathbb{Z} \right\} $$ and taking the sum $$ \sum_{r\in R} \frac{1}{r^{h+1}} = \sum_{n = 1}^\infty \alpha^{n(h+1)} \sum_{k \in \mathbb{Z}} \frac{1}{\left|\frac{\pi}{2} + \pi k\right|^{h+1} } $$ we note that the $k$ sum is a $p$ series with $p = h+1$, hence this forces $h \geq 1$, and if this is the case the $n$ series is a multiple of a convergent geometric series as $0 < \alpha < 1$, showing $h = 1$.
Finally, to compute the order we simply note that $\cos(z)$ is of order $1$ and hence $$ \prod_{n=1}^\infty |\cos(\alpha^n z)| \leq C\prod_{n=1}^\infty e^{\alpha^n |z|} = Ce^{|z| \sum_{n=1}^\infty \alpha^n}$$ hence the order of our product is $\leq 1$. From here, we note that by Hadamard's theorem $1 = h \leq \lambda \leq 1$ allowing us to arrive at an order of $\lambda = 1$.

Problem 3 (Prelim August 2021)

Let $f$ be a meromorphic function on $\mathbb{C}$ satisfying $f(z)f(-z) = 1$ for all $z\in \mathbb{C}$. Show that there exists an entire function $g$ such that $f(z) = g(z)/g(-z)$ for all $z\in \mathbb{C}$. (For simplicity you may assume that $f(0) = 1$.)

Hint Note that we do not necessarily have that $f$ is rational (for instance, we could have $f(z) = e^z$.) However, all meromorphic functions are quotients of two entire functions. Write their canonical products.
Solution Choosing entire functions $p,q$ such that $f = p/q$ we note by our equality that a zero $f$ at $z$ corresponds to a pole of equal order at $-z$ and vice versa. Hence, if $\{z_i\}_{i=1}^N$ are the roots of $p$ then $\{-z_i\}_{i=1}^N$ are the roots of $q$ ($0 \leq N \leq \infty$.) This gives the canonical products $$ \begin{align*} p(z) &= e^{g_1(z)} \prod_{i=1}^N \left(1-\frac{z}{z_i} \right) e^{p_i(z/z_i)} \\ q(z) &= e^{g_2(z)} \prod_{i=1}^N \left(1+\frac{z}{z_i} \right) e^{p_i(-z/z_i)} \\ \end{align*} $$ where $g_1,g_2$ are entire functions without $0$ in their image. Computing the product in the hypothesis we find $$1 = f(z)f(-z) = \frac{e^{g_1(z)}e^{g_1(-z)}}{e^{g_2(z)}e^{g_2(-z)}} $$ and taking the complex logarithm we find we must have $$ (g_1(z) + g_1(-z)) - (g_2(z) + g_2(-z)) = 2\pi i n$$ for some $n\in \mathbb{Z}$. from here we can define $$g(z) = e^{[g_1(z) - g_2(z)]/2} \prod_{i=1}^N \left(1-\frac{z}{z_i} \right) e^{p_i(z/z_i)}$$ and we see that $$ \begin{align*} \frac{g(z)}{g(-z)} &= e^{[g_1(z) - g_2(z)]/2 - [g_1(-z) - g_2(-z)]/2} \prod_{i=1}^N \left(1-\frac{z}{z_i} \right)\left(1 + \frac{z}{z_i} e^{p_i(z/z_i) + p_i(-z/z_i)}\right) \\ &= e^{[g_1(z) - g_2(z)]/2 + [g_1(z) - g_2(z)]/2 + \pi i n} \prod_{i=1}^N \left(1-\frac{z}{z_i} \right)\left(1 + \frac{z}{z_i} e^{p_i(z/z_i) + p_i(-z/z_i)}\right) \\ &= \pm f(z) \end{align*} $$ Finally, we note that since $f(0) = 1$ that $g_1(0) - g_2(0) = 2\pi i k$ for some $k \in \mathbb{Z}$, and it follows immediately that $n = 2k$, and hence $g(z)/g(-z) = +f(z)$ as desired.

Problem 4 (Prelim August 2021)

Let $f$ be an entire function satisfying a bound $|f(z)| \leq \text{exp}(|z|^n)$ for all $z\in \mathbb{C}$, where $n$ is some positive integer. If $f(z) = 0$ whenever $\text{exp}(\text{exp }z) = 1$ show that $f = 0$.

Hint We have enough information to compute $f$'s order and genus.
Solution We see that $f$'s order $\lambda \leq n$. Additionally, $\text{exp}(z) = 1$ for all $z = 0 + 2\pi i j$, $j\in \mathbb{Z}$ and the preimages of these over $\text{exp}$ is the set $$ \left\{ \log(2\pi |j|) + \left(\frac{\pi}{2} + 2\pi k\right) i : j,k \in \mathbb{Z} \right\}$$ since these are roots of $f$ we see $f$'s genus must be bounded below by the smallest integer $h$ such that $$ \sum_{j,k\in \mathbb{Z}} \frac{1}{\sqrt{\log(2\pi j)^2 + 4 \pi^2 k^2 + \pi^2/4+2\pi^2k}^{h+1}} < \infty $$ and clearly the $\log$ term can cause some issues with convergence. To focus on this, note that the sum is bounded below by the sum of terms with $k = 0$, $j \geq 2$. Over this interval the above sum behaves similarly to $$ \sum_{n=2}^\infty \frac{1}{\log(j)^{h+1}} \geq \int_{2}^\infty \frac{1}{\log(x)^{h+1}} = \int_{\log 2}^\infty \frac{e^u}{u^{h+1}} = \infty $$ hence the genus of $f$ is not finite. This would contradict Hadamard's theorem if $f$ were non-constant, hence $f \equiv 0$.

Problem 5 (Prelim August 2014)

Find a function $f$ holomorphic on $\mathbb{C} \setminus \mathbb{N}$ with a pole of order $n$ at $z = n$ for all positive integers $n$.

Hint Find a canonical product corresponding to the zeros of $1/f$.
Solution Calculating the genus of a function with a zero of order $n$ at every positive integer $n$ we find $$ \sum_{n=1}^\infty \frac{n}{n^{h+1}} = \sum_{n=1}^\infty \frac{1}{n^h}$$ and by $p$ test we see it is of genus $2$. The general form of a function of genus 2 is $$ g(z) = Ce^{\alpha z}\prod_{n = 1}^\infty \left(1-\frac{z}{z_i}\right)e^{z/z_i}$$ and in our case we can let $$ g(z) = \prod_{n=1}^\infty \left[\left(1-\frac{z}{n}\right) e^{z/n}\right]^n $$ be our function with prescribed roots of order $n$ at $n\in \mathbb{N}$. We can then take $f = 1/g$.

Problem 6 (Prelim August 2020)

Prove that [ \frac{\pi^2}{\sin^2(\pi z)} = \sum_{n=-\infty}^\infty \frac{1}{(z-n)^2} ]

Hint Apply Mittag-Leffler, try to bound the resulting entire function on a single strip $0 \leq \text{Re}(z) \leq 2\pi$.
Solution We see that there is a pole of order two at every $z \in \mathbb{Z}$. We will first compute the singular part of the function at $z = 0$. At this point, note that its reciprocal $\sin^2(\pi z)/\pi^2$ has a double root and second derivative 1 at $z = 0$, hence the singular part at $z = 0$ is $$ \frac{1}{z^2} $$ and due to our function being a $1$-periodic function the singular part at $z =n$ must be $$ \frac{1}{(z-n)^2}.$$ Next note that on any compact subset $K\subset \mathbb{C}\setminus \mathbb{Z}$ we have a uniform bound $|z| < M$. Then for $|n| > M$ we find $$ \frac{1}{|z-n|^2} \leq \frac{1}{(M - |n|)^2}$$ which converges by $p$-test. The M-test establishes uniform convergence on $K$ and now Mittag-Leffler guarantees the existence of an entire function $g$ such that $$ \frac{\pi^2}{\sin^2(\pi z)} = g(z) + \sum_{n=-\infty}^\infty \frac{1}{(z-n)^2}.$$ Note that both the left hand side and the sum of singular parts is $1$-periodic, hence so is $g$. Taking the limit as $\text{Im }z \to \infty$ we see $\sin^2(\pi z), \sum (z-n)^{-2} \to 0$. This establishes that that we can bound $g$ on the sytip $0 \leq \text{Re}(z) \leq 1$ which then by periodicity establishes a bound on all of $\mathbb{C}$. This then forces $g$ to be constant by Liouville's theorem, and since the limits as $z\to \infty$ are both zero we see that $g \equiv 0$.

Problem 7 (Prelim January 2013)

Determine the partial fraction expansion for [ \frac{1}{\sqrt{z} \sin \sqrt{z}} ]

Hint While the appearance of the square root makes it seem like you must work with branches, consider the degree of terms in the Taylor series expansion of $w\sin w$. Does it matter which branch is chosen?
Solution As mentioned in the hint, the map $w\mapsto w\sin w$ has a Taylor expansion of only even powers of $z,$ so we can just imagine the square root halving these powers.
This map isn't periodic so we can't replicate the reasoning in problem 6 to show $g$ is constant in this functions Mittag-Leffler expansion. Instead, let us consider the integral formula over an appropriate contour $$ \int_{R_N} \frac{1}{\xi - z} \frac{1}{\xi \sin (\xi )} \,d\xi $$ We know that when $z$ is not a pole of our meromorphic function ($z \notin \pi \mathbb{Z}$) then we can place a small circular contour around the function such that this integral evaluates to $2\pi i/(z \sin z)$. If we let $R_N$ be a large rectangle connecting to our small circular contour then we will be able to relate the sum of residues in the integral formula expression, $1/(z \sin z)$, and the integral over $R_N$. We will define the contour for $N \in \mathbb{N}$ by $$ R_N = \partial \left\{x + iy : |x| < \pi N^2+ \frac{\pi}{2}, |y| < N \right\}$$ (the choice of real and imaginary bounds will become clear once we bound the integral.)
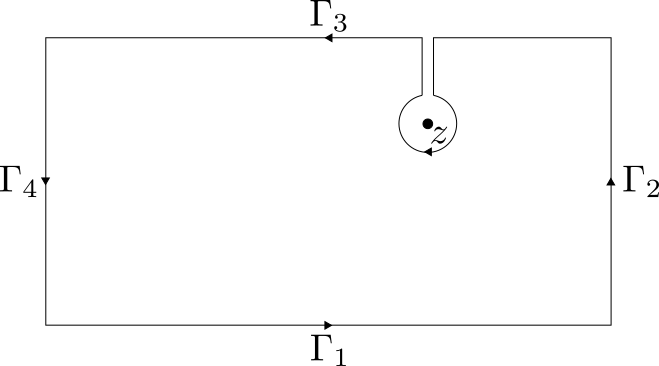
Square contour
Then by the residue theorem $$ \int_{R_n}\frac{1}{\xi - z} \frac{1}{\xi \sin (\xi )} \,d\xi - 2\pi i \frac{1}{z\sin(z)} = 2\pi i\sum_{n = -N^2}^{N^2} \text{Res}_{z = \pi n}(f) $$ where $f$ is the integrand. For $n \ne 0$ we see $$ \text{Res}_{z = 2\pi n}(f) = \lim_{\xi \to \pi n} \frac{\xi - \pi n}{\xi - z} \frac{1}{\xi \sin(\xi)} = \frac{(-1)^n}{(\pi n-z) \pi n} $$ and when $n = 0$ $$ \text{Res}_{z = 0}(f) = \lim_{\xi \to \pi n} \frac{d}{d \xi} \frac{\xi^2}{\xi - z} \frac{1}{\xi \sin(\xi)} = \frac{1}{z^2}.$$ Finally, if we can show the integral term converges to zero as $N \to \infty$ we will have a partial fractions decomposition of our function. Dividing $R_n$ into $\Gamma_1,\Gamma_2, \Gamma_3,\Gamma_4$ (as it is in the picture) we can apply the ML-lemma twice. Indeed, over either $\Gamma_1 + \Gamma_3$ $$ \left|\int_{\Gamma_1} f(\xi)\,d\xi\right| \leq L(\Gamma_1) \sup_{z \in \Gamma_1} |f(z)| \leq (2N^2+1)\pi \frac{2}{N \sinh(N)} \to 0$$ as $n\to \infty.$ Now for the vertical segments we note that since $x = \pm \pi (N^2 + 1/2)$ we have $$ \begin{align*} \sin(x + iy) &= \frac{e^{i(\pi N^2 + \pi/2) - y} - e^{-i(\pi N^2 + \pi/2) + y}}{2} \\ &= (-1)^N i \frac{e^{-y} + e^y}{2} = (-1)^N i \cosh(y) \end{align*} $$ and since $\cosh$ has minimum value $1$ the ML-lemma on $\Gamma_2$ and $\Gamma_4$ gives $$ \left|\int_{\Gamma_2} f(\xi)\,d\xi\right| \leq L(\Gamma_2) \sup_{z \in \Gamma_2} |f(z)| \leq 2N \frac{1}{\pi N^2} \to 0$$ as $N\to \infty$. As a result, taking the limit as $N\to \infty$ of residue theorem expression yields $$ \frac{1}{z\sin(z)} = \frac{1}{z^2} + \lim_{N\to \infty}\sum_{n=-N}^N \frac{(-1)^n}{(z-\pi n)\pi n} = \frac{1}{z^2} + \lim_{N\to \infty}\sum_{n=-N}^N (-1)^n\frac{2}{z^2-(\pi n)^2} $$ and since all powers of $z$ are even we can substitute in the square root, simply halving these powers.

Problem 8 (Prelim January 2019)

Prove that [ \frac{d}{dz} \left( \frac{\pi \sin(z)}{\sin(\pi z)} \right) = \sum_{n=-\infty}^\infty \frac{(-1)^{n+1} \sin(n)}{(z-n)^2} ] for all $z\in \mathbb{C}\setminus \mathbb{Z}$, with the sum on the right hand side converging uniformly on every compact subset of $\mathbb{C}\setminus \mathbb{Z}$.

Hint This function will provide a nasty decomposition if we just use Mittag-Leffler. Instead consider computing the derivative using the integral formula, then expanding the contour we will gain an "error" equal to the sum of some residues.
Solution We will slightly modify the contour from problem 7 to $$ R_N = \partial \left\{x + iy : |x| < N^2+ \frac{1}{2}, |y| < N \right\} $$ and note we have the relationship $$ \int_{R_n}\frac{1}{(\xi - z)^2} \frac{\pi \sin(\xi)}{\sin (\pi \xi)} \,d\xi - 2\pi i \frac{d}{d\xi} \left(\frac{1}{\xi\sin(\xi)}\right)_{\xi = z} = 2\pi i\sum_{n = -N^2}^{N^2} \text{Res}_{z = \pi n}(f) $$ where $f$ is the integrand on the left. We have poles at every $\xi\in \mathbb{Z} \setminus \{0\}$, at $\xi = n$ we find the residue $$ \text{Res}_{\xi = n}(f) = \lim_{\xi \to n} \frac{\xi - n}{(\xi - z)^2} \frac{\pi \sin(\xi)}{\sin (\pi \xi)} = \frac{(-1)^{n}\sin(n)}{(z-n)^2} $$ From here we just need to show the integral shrinks to zero as $N\to \infty$. Indeed, for $\Gamma_1,\Gamma_3$ the ML-lemma gives $$ \left| \int_{\Gamma_1} f\,d\xi\right| \leq L(\Gamma_1)\sup_{z\in \Gamma_1}|f(z)| \leq (2N+1) \frac{\pi \cosh(N)}{\sinh(\pi N)} \to 0$$ as $N\to \infty$ as $\pi > 1$. Now for the vertical segments $\Gamma_2, \Gamma_4$ we can employ the same lower bound on $\sin$ over these segments as was used in problem 7. We see $$ \left| \frac{\pi \sin(z)}{\sin(\pi z)} \right| \leq \left| \frac{\pi \cosh(y)}{\cosh(\pi y)} \right| \leq \pi $$ when $\text{Re}(z) = N^2 + 1/2$ hence the ML-lemma gives $$ \left| \int_{\Gamma_2} f\,d\xi\right| \leq L(\Gamma_2)\sup_{z\in \Gamma_2}|f(z)| \leq 2N \frac{\pi \cosh(N)}{\cosh(\pi N)} \to 0$$ as $N \to \infty$. This establishes the equality $$ \frac{d}{dz} \left( \frac{\pi \sin(z)}{\sin(\pi z)} \right) = \sum_{n=-\infty}^\infty \frac{(-1)^{n+1} \sin(n)}{(z-n)^2} $$ pointwise. If $K$ is any compact set avoiding the poles of our function then for all $z\in K$ we have $|z| < M$. We can then see that for indices $n > M$ we have $$ \left| \frac{(-1)^{n+1} \sin(n)}{(z-n)^2} \right| \leq \frac{1}{(M - n)^2} $$ and for $n < -M$ we find $$ \left| \frac{(-1)^{n+1} \sin(n)}{(z-n)^2} \right| \leq \frac{1}{(-M - n)^2} $$ In both cases the modulus of the terms are $O(n^{-2})$ and we know $\sum_{n=1}^\infty n^{-2}$ is a convergent series, hence by the M-test convergence over $K$ is uniform.

Problem 9 (Prelim January 2017)

Determine the partial fractions expansion of [ \frac{1}{z\sin z} ]

Solution As shown in problem 7, $$\frac{1}{z\sin z} = \frac{1}{z^2} + \sum_{n=1}^\infty (-1)^n \frac{2}{z^2 - (n\pi)^2}$$

Problem 10 (Prelim January 2016)

Determine all entire functions $f$ satisfying $f(\sqrt{n}) = n$ for all positive integers and $|f(z)| \leq e^{3|z|}$ for every complex number $z$.

Hint From our problem statement we can find the order of $z\mapsto f(z) - z^2$.
Solution Clearly $|f(z) - z^2| \leq Ce^{3|z|}$ for some $C > 1$ hence $f(z) - z^2$ is of order $1$. The solutions of $f(z) = z^2$ includes $\sqrt{n}$ for all $n \in \mathbb{N}$, hence the genus is bounded below by the smallest integer $h$ such that the series $$ \sum_{n = 1}^\infty \frac{1}{\sqrt{n}^{h+1}} $$ converges. By the $p$-test we must have $(h+1)/2 > 1$ hence $h = 2$ is the smallest integer giving convergence. It follows that $f(z) -z^2 \equiv 0$, for if not we will have $\lambda < h$ violating Hadamard's theorem.

Problem 11 (Prelim January 2014)

Assume $f$ is entire and of finite order. Prove that if $|f(z)| \leq 1$ for all $z$ in the boundary of the half-strip [ S = \{z \in \mathbb{C}: \text{Re}(z) \geq 0, |\text{Im}(z)| \leq 1 \} ] then $|f(z)| \leq 1$ for all $z\in S$.

Hint Consider the collection on functions $f(z)e^{-\epsilon z^n}$ for an appropriate choice of $n$ and $\epsilon > 0$.
Solution $f$ being of order $\lambda$ implies that for all $\alpha > \lambda$ we have $f(z) \leq C e^{|z|^\alpha}$ for some $C>0$ and suitably large $z$. Choose $n$ to be the smallest integer greater than $\lambda$. Then for every $\epsilon > 0$ we see for sufficiently large $z$ that $$|f(z) e^{-\epsilon z^{n+1}}| \leq Ce^{|z|^n} e^{-\epsilon \text{Re} z^{n+1}}$$ Writing $z^{n+1} = |z|^{n+1}e^{i(n+1)\theta}$ we observe that elements of $S$ with higher real part have the possible values for $\theta$ converge to $0$, hence for large enough $z$ will find $\text{Re} z^{n+1} > |z|^{n+1}/2$. Since our upper bound $Ce^{|z|^n - \epsilon |z|^{n+1}/2} \to 0$ as $|z| \to \infty$ we can select $L$ such that this bound $\leq 1$ for all $\text{Re}(z) \geq L$. Then in the regions $\{z\in S: \text{Re}(z) \leq L'\}$ where $L' \geq L$ we can apply the maximum modulus principle to bound $|f| \leq 1$ in the set. Since we can pick any $L' \geq L$ this bound holds on the entire set $S$.
Finally, given a compact set $K \subset S$ we will find $|z| \leq M$ for some $M > 0$. Now by the triangle inequality, $$\sup_{z\in K} |f(z)e^{-\epsilon z^{n+1}} - f(z)| \leq \sup_{z\in K} |f(z)| (e^{\epsilon M^{n+1}} -1) \to 0$$ as $\epsilon \to 0$. Since we converge uniformly on compact sets and every function $f(z)e^{-\epsilon z^{n+1}}$ is uniformly bounded by $1$ it follows that $f$ has this bound as well.

Problem 12 (Prelim August 2017)

Let $D_2 \subset D_1$ be two disks in $\mathbb{C}$ with $D_1$ open and $D_2$ closed. Let $f$ be an analytic function on $D_1\setminus D_2$. Show that there exist holomorphic functions $f_1$ on $D_1$ and $f_2$ on $\mathbb{C} \setminus D_2$ such that $f = f_1 + f_2$ on $D_1\setminus D_2$.

Hint Consider the integral formula over an appropriate region to construct the $f_i$.
As an aside, this construction for disks with the same center is used to find Laurent series where the positive powers arise for $f_1$ and negative powers from $f_2$.
Solution Choose circular contours $C_1,C_2$ where $C_1 \subset D_1$ is a slightly smaller concentric circle to the boundary of $D_1$ while $C_2$ is a slightly larger concentric circle to $D_2$. We will also give $C_1$ and $C_2$ circles positive and negative orientation, respectively.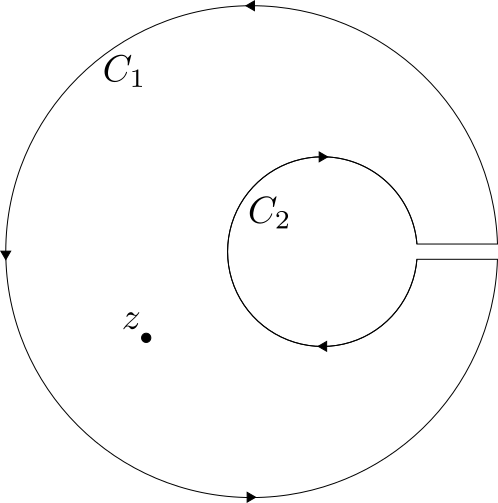
A contour connecting two circles, one contained within the other.
We see that the interior of the path formed by their disjoint union is contained in $D_1\setminus D_2$ hence we can apply the integral formula $$ f(z) = \int_{C_1} \frac{f(\xi)}{\xi - z}\,d\xi + \int_{C^2} \frac{f(\xi)}{\xi - z}\,dx =: f_1(z)+f_2(z). $$ The functions $f_i$ are holomorphic by the general theory set out in Ahlfors 4.2. Outlining for $f_1$, we can show $f_1$ is continuous and then directly compute the derivative via difference quotient $$ \begin{align*} f_1'(z) &= \lim_{z'\to z} \frac{f_1(z) - f_1(z')}{z-z'} \\ &= \lim_{z'\to z} \frac{1}{z-z'}\int_{C_1} \frac{(z-z')f(\xi)}{(\xi-z)(\xi-z')} = \int_{C_1} \frac{f(\xi)}{(\xi-z)^2}\,d\xi \end{align*}$$ As a final note, while the sets $C_i$ do not enclose the entire regions $D_i$ we can select $C_i$ closer and closer to $\partial D_i$ and extend the $f_i$ by analytic continuation.